-
随着激光雷达(LiDAR)技术的快速发展，精度极高的三维点云数据被广泛应用于多个领域以提取真实世界的信息[1]。地面激光雷达(TLS)作为一种常用的主动遥感技术，可以有效地穿透森林冠层，实现非破坏性的高分辨率三维测量[2]。地面激光雷达获取的树木点云可帮助林业工作者轻松提取林业参数，如胸径、树高、叶面积指数、树冠体积、树枝和树干生物量、林分蓄积量等[3−11]。此外，借助激光雷达数据和更先进的算法提取单木骨架，不仅有助于开展单木生长状态监测和结构参数估算，还能为优化林分结构提供数据支持，推动林业精细化管理和生态系统的可持续发展。
三维树木建模包括树枝建模与树叶建模，其中决定树木整体形态的树枝建模尤为重要。树枝建模方法目前主要有2种：Delaunay三角剖分方法和骨架方法。使用Delaunay三角剖分生成的模型在视觉上更为真实，但在提取林业参数方面存在困难，且形态参数的误差较大[12]。骨架方法能完整表达物体的形状，同时保持其原有形状的连通性和拓扑结构的分布特征，该方法应用十分广泛[13]。
为了从点云中提取树木骨架，研究人员在野外实验中测试了多种创新方法。根据不同方法的原理，树木点云骨架结构的提取方法大致可分为3类：基于图论、空间分割和形态学原理的方法。第1类方法是基于局部点云分割和聚类来计算骨架节点，再利用图论原理连接这些节点进而生成树木骨架。HUANG等[14]采用聚类算法提取树枝中心点，结合Dijkstra算法构建树骨架，并通过圆柱体模型和角度优化规则重建树干分枝结构。JIANG等[15]提出了一种基于图收缩的能量优化方法，通过最小化k最近邻和局部主方向约束压缩点云，再利用骨架节点连接算法构建拓扑正确的树木骨架。第2类方法是通过对点云三维空间进行分割，获得如体素等新的度量单元，然后通过细化和收缩来计算骨架节点并生成骨架。BUCKSCH等[16]采用基于八叉树图提取、图简化及骨架嵌入的3步方法，通过单参数控制构建树木骨架，但该方法无法处理数据缺失问题。FU等[17]基于八叉树和水平集提取初始骨架，利用圆柱先验约束(CPC)和分支半径优化节点位置，确保拓扑正确性。第3类方法是基于对象自身结构特征的形态学原理。AI等[18]借鉴了X射线计算机断层扫描的医学成像技术，提出了一种基于多视图切片的树木骨架自动提取方法，但该方法生成的骨架连通性较差，且受树木遮挡和缺失数据限制。GAO等[19]通过力场驱动将点云表面测地线压缩成骨架，并优化得到树木骨架，但也无法处理断枝问题。此外，还有一些学者通过结合不同方法构建骨架，定量结构模型(QSM)重建算法便是通过树枝骨架来构建三维树木模型并计算体积[20]。如FAN等[21]基于TreeQSM改进版本的AdQSM模型，通过将Delaunay 三角剖分和图论方法相结合连接骨架节点，提升了树枝区域的骨架连通性。综上所述，现有方法在一定程度上实现了树木骨架提取，但在拓扑保真、精度、自动化和鲁棒性方面仍存在不足。首先，一些方法在粗细结构共存时易发生收缩失衡，难以保持拓扑结构的完整性。其次，部分方法在节点密度和间隔精度上表现不佳，导致骨架细节欠缺。第三，一些方法需要人工干预，降低了自动化程度，增加了使用成本[22]。第四，面对噪声、离群点和遮挡等问题时，现有方法难以保持稳定性能，鲁棒性有待提升。
针对现有树木骨架提取方法存在的保真度较低、拓扑结构完整性较差等问题，本研究提出了一种基于地面激光雷达点云的树木骨架提取方法。首先采用多站地面激光扫描技术获得树木点云，以增强获取树木完整结构的能力。在点云预处理与枝叶分离的基础上，再利用基于拉普拉斯收缩算法(LBC)的语义骨架化方法，有效保留并表达细小分支的拓扑特征，获得高保真、拓扑正确的树木骨架结构，为树木三维建模及生态参数计算提供了可靠的技术支撑。
-
于2024年11月在浙江农林大学校园及其附近进行数据采集。选取3株不同种类的树木样本(山核桃Carya cathayensis、银杏Ginkgo biloba和刺槐Robinia pseudoacacia)进行模型验证与分析。所选样本均为成年个体，树高为3~5 m，胸径为40~60 cm。为便于表述，后续分析中分别以树1、树2和树3指代上述样本。为确保数据的全面性和精确性，选用Trimble X7三维激光扫描仪采集数据，其参数如表1所示。考虑到树木叶片与枝干可能存在聚集和遮挡等复杂因素，特别选择在秋季进行数据采集。此时大多数落叶树已开始落叶，避免叶片遮挡问题，确保枝干结构的完整性和准确性。为进一步减少树叶对点云数据采集的干扰，并避免过于密集的点云影响后续处理，采集工作在晴朗无风的天气条件下进行。
表 1 Trimble X7仪器参数
Table 1. Detailed parameters of Trimble X7 scanner
指标 参数 指标 参数 扫描EDM激光类别 1类激光，对人眼安全，符合IEC EN60825-1标准 测程 0.6~80.0 m 激光波长 1 550 nm，不可见 高灵敏度模式 暗色(沥青)和反光(不锈钢)表面 视场 360°× 282° 精度验证 具有自动校准，终身保证 扫描时间 最快2 min 34 s(带影像)，1 min 34 s(无影像) 测距精度 2 mm 扫描速度 最大500 kHz 角度精度 21′′ 测量原理 高速、数字飞行时间测距技术 3D点精度 2.4 mm@10 m，3.5 mm@20 m，6.0 mm@40 m 测距噪声 ＜3 mm@60 m，80%反射2 在树木周围布设多个独立测站进行环绕扫描，确保各测站能够全面覆盖被测区域，以获得完整的三维点云数据。扫描距离设定为50 m以内，单次扫描时间为1 min 34 s，未采集RGB影像。在浙江农林大学南门、玉兰路和全国重点实验室前后共4个不同场景下采集点云数据。数据采集完成后，使用Trimble X7配备的现场数据处理软件Trimble Perspective对不同测站的扫描数据进行自动配准，最终整合出完整的实验场景数据。
-
本研究提出树木骨架提取算法，首先，从整个扫描场景中手动分割单株树木，并进行希尔伯特曲线(HC)下采样[23−24] 和降噪处理；其次，采用LeWoS模型进行枝叶分离，提取清晰的树干点云；最后使用拉普拉斯收缩算法提取和优化树木骨架。
-
对配准后的点云数据使用CloudCompare商业软件进行手动分割，提取多个树种的单株树木的完整点云作为建模算法的输入。
-
激光雷达扫描得到的点云数据是对真实场景中的物体进行采样的结果，在扫描采样的过程中会受到外界环境、目标物体表面形状纹理等因素的影响[25]。1株树的点云数据包含数十万个点，为了在保留数据关键特征的同时，降低计算复杂度并提高后续处理的效率，本研究在降噪的基础上采用基于希尔伯特曲线下采样方法进行数据处理。在希尔伯特曲线下采样中，首先对点云进行归一化，将其映射到[0, 1]3空间，并划分为多个子区域。然后，利用[0, 1]和[0, 1]d之间的分区映射关系，将每个子区域中的点投影到中心位置，其中，d表示点云数据的维度。对于那些投影到相同位置的点，会根据局部点云密度进行筛选，最终保留能代表局部结构特征的点。为了保持点云在空间上的均匀分布，希尔伯特曲线依据每个子区域内的点数(Nh)计算采样比例，确保不同区域的点云稀疏程度尽量保持一致。下采样后，点云的整体分布仍尽可能接近原始点云的结构特性。下采样后目标点数量的计算公式为：
$$ {N}_{{\mathrm{h}}}=\frac{{N}_{{\mathrm{s}}}}{{B}_{\mathrm{i}\mathrm{n}\mathrm{s}}} 。 $$ (1) 式(1)中：Nh为每个子区域内的点数；$ N_{\mathrm{s}} $是下采样后目标点的数量；Bins是分块的数量，即希尔伯特曲线在下采样过程中将点云划分的空间单元数量。直观上，选定的点近似均匀分布在原始空间中，从而能够有效地保留树的结构特征。
-
树木骨架的提取是三维树木建模的核心环节。为实现形态合理且分布均匀的高精度树木骨架的提取，首先使用拉普拉斯收缩算法对枝干点云进行处理，以收缩点云并构建树木的初始骨架，再通过“树枝平滑”技术对初始骨架进行优化，改善其形态的平滑性和连通性。
-
树木的枝干和叶片在几何形态和生物特征上存在明显差异，而激光雷达点云数据仅包含坐标和强度信息，需要对枝干和叶片进行类别判断。为此，本研究采用LeWoS模型[26]进行枝叶分离。
LeWoS模型结合了几何特征分析和拓扑推理，通过多尺度分析对点云数据进行枝叶分离。首先，通过计算每个点的局部密度初步区分枝干与树叶，其中枝干通常位于密度较高的区域，树叶则集中在密度较低的区域。其次，利用局部曲率进一步区分枝干和树叶。局部曲率通过拟合邻域点的Hessian矩阵进行量化，反映了表面的弯曲程度。由于树叶的形态较为复杂，其局部曲率较高，枝干则表现为相对平滑的表面。最后，LeWoS综合局部密度和曲率信息，通过加权评分函数为每个点分配权重，并结合动态阈值判断点的归属，从而实现枝干和树叶的有效分离。
-
通过枝叶分离得到枝干点云后，为重建树木枝干的三维模型，使用拉普拉斯收缩算法[27]从枝干部分的点云中提取骨架点。拉普拉斯收缩算法通过对点云施加松弛压缩，减少噪声和不规则性，使输入点云$ \boldsymbol{C}\in {{R}}^{{N}_{{\mathrm{C}}}\times 3}(\mathrm{其}\mathrm{中}{N}_{{\mathrm{C}}} $是树的点数)收缩至紧凑的点集，并迭代求解拉普拉斯矩阵方程，最终获得收缩点云。然而，拉普拉斯收缩算法在处理枝干模型时存在不足。首先，对于径差较大的树干与树枝，拉普拉斯收缩算法易出现不良收缩，使树木结构细节丢失，影响树枝的拓扑保持。其次，在点云数据存在缺失的情况下，拉普拉斯收缩算法可能无法准确处理树干连接关系，导致骨架结构错误。因此，拉普拉斯收缩算法在处理复杂树木结构时难以兼顾枝干细节与拓扑完整性，从而影响最终模型的精度和真实感。
为了解决上述问题，本研究选用基于语义拉普拉斯算子的收缩算法(S-LBC)[28]，将点云的语义信息有效地整合到拉普拉斯收缩算法中，从而优化骨架提取过程。该方法的核心创新在于将点云的语义分割信息，如主干点云($ {\boldsymbol{C}}_{\mathrm{T}} $)和分支点云($ {\boldsymbol{C}}_{\mathbf{B}} $)的分类结果，融入传统拉普拉斯框架。具体实现中，通过构建语义加权矩阵$ \boldsymbol{S}\in {{R}}^{N_{\mathrm{C}}\times N_{\mathrm{C}}} $，对主干和分支点云分别施加不同的收缩权重：主干点赋予较大权重($ {\lambda }_{\mathrm{T}} $)以增强收缩效果，保持主干的粗壮形态；分支点则统一设为权重1以避免过度收缩，从而保留树枝的细节结构。此外，算法通过拉普拉斯矩阵($ \boldsymbol{L} $)中的子矩阵(LC)显式建模主干与分支间的连接关系，确保拓扑结构的正确性。
-
初步提取的骨架易受噪声、拓扑不连续和形态不规则等问题的影响。为此，本研究采用拉普拉斯平滑算法对骨架进行优化，以提高树木建模的精度。拉普拉斯平滑算法旨在通过点之间的相对几何关系调整每个点的位置，从而使点云的形状更加平滑，并符合自然的几何分布。利用该方法对树木初始骨架中每个顶点的邻居点进行加权平均，更新顶点的位置，更新的权重由顶点与其邻居之间的距离决定。距离越近，邻居对该顶点的影响力就越大。该方法通过多次迭代，使得点云逐渐消除局部噪声和拓扑不规则，改善了树木骨架的平滑性与结构。拉普拉斯平滑的基本迭代公式为：
$$ {\upsilon }_{i}^{\mathrm{n}\mathrm{e}\mathrm{w}}=\alpha \left(\sum _{j\in N\left(i\right)}{\omega }_{ij} {\upsilon }_{j}\right)+(1-\alpha ) {\upsilon }_{i}^{\mathrm{o}\mathrm{l}\mathrm{d}}\mathrm{。} $$ (2) 式(2)中：$ {\upsilon }_{i}^{\mathrm{n}\mathrm{e}\mathrm{w}} $表示更新后的顶点位置；$ {\upsilon }_{i}^{\mathrm{o}\mathrm{l}\mathrm{d}} $为当前的顶点位置；$ {\upsilon }_{j} $为顶点的$ j $邻居点；$ {\omega }_{ij} $是顶点$ i $与邻居点$ j $之间的权重；$ \alpha $为平滑系数。目标顶点的位置在每次迭代中都根据其邻居点的加权平均位置进行调整，最终实现平滑效果。
-
为了全面评估与比较希尔伯特曲线下采样、随机下采样和网格下采样3种方法的性能，本研究在保持相同下采样率(90%)条件下，选取了Hausdorff距离、计算时间和点密度保留度作为评价指标。Hausdorff距离[$ {d}_{\mathrm{H}}({A},{B}) $]和点密度保留度(R)的计算公式如式(3)、式(4)所示：
$$ {d}_{\mathrm{H}}({A},{B})=\mathrm{m}\mathrm{a}\mathrm{x}\left\{_{a\in A}^{\mathrm{s}\mathrm{u}\mathrm{p}} \;{}_{b\in B}^{\mathrm{i}\mathrm{n}f}\|a-b\|,\;{}_{a\in A}^{\mathrm{s}\mathrm{u}\mathrm{p}} \;{}_{b\in B}^{\mathrm{i}\mathrm{n}f}\|b-a\|\right\} 。 $$ (3) 式(3)中：$ A $和$ B $分别表示原始点云和下采样后的点云；a为原始点云A中的任意一个点；b为原始点云B中的任意一点；$ \|\cdot \| $为欧几里得距离。距离越小，表明下采样后点云与原始点云的几何一致性越高。
计算时间反映了下采样过程的效率，能够直观展示方法的计算成本。
$$ R=\frac{{N}_{\mathrm{S}}}{{N}_{\mathrm{O}}}\times 100\%\mathrm{。} $$ (4) 式(4)中：$ {N}_{\mathrm{O}} $为原始点云的点数，$ {N}_{\mathrm{S}} $为下采样点云的点数。R越大，表明点云的局部特征保留得越完整。
-
为定量评估LeWoS模型的性能，分别选用总体准确率(Ac)、精确率(Pr)、召回率(Re)和F1 值作为评价指标。上述评价指标的具体计算公式如下：
$$ {A}_{\mathrm{c}}=\frac{{T}_{\mathrm{P}}+{T}_{\mathrm{N}}}{{T}_{\mathrm{P}}+{T}_{\mathrm{N}}+{F}_{\mathrm{P}}+{F}_{\mathrm{N}}}\times 100\%\text{；} $$ (5) $$ {P}_{\mathrm{r}}=\frac{{T}_{\mathrm{P}}}{{T}_{\mathrm{P}}+{F}_{\mathrm{P}}}\times 100\%\text{；} $$ (6) $$ {R}_{\mathrm{e}}=\frac{{T}_{\mathrm{P}}}{{T}_{\mathrm{P}}+{F}_{\mathrm{N}}}\times 100\%\text{；} $$ (7) $$ {F}_{1}=2\times \frac{{P}_{\mathrm{r}}\times {R}_{\mathrm{e}}}{{P}_{\mathrm{r}}+{R}_{\mathrm{e}}}\times 100\% 。 $$ (8) 式(5)~(8)中：TP为正确分类的枝叶点；TN为正确分类的非枝叶点；FN为非枝叶点被误分类为枝叶的数量；FP为枝叶点被误分类为非枝叶的数量。
-
为了对比最小生成树(MST)算法、L1算法、拉普拉斯收缩算法(LBC)与基于语义拉普拉斯收缩算法(S-LBC)的性能，选用骨架节点数量、平均点云间隔以及运行时间作为评价指标。
骨架节点数量反映了骨架结构的复杂性和细节保留程度。节点越多，说明骨架对原始点云的几何特征(如细小分支、树冠过渡区域等)捕捉越精细。
平均点云间隔为所有相邻骨架点之间的欧氏距离的平均值(Av)，其公式如下：
$$ {A}_{\mathrm{v}}=\frac{1}{N-1}\sum _{i=1}^{N-1}\parallel {\boldsymbol{p}}_{i+1}-{\boldsymbol{p}}_{i}\parallel \mathbf{。} $$ (9) 式(9)中：$ N $为骨架节点数，$ {\boldsymbol{p}}_{i} $为骨架中第i个节点坐标。
运行时间用来评估算法的计算效率，反映实际应用的可行性。时间越长，算法复杂度越高。
-
为定量评价骨架优化效果，本研究选用节点数、边数、连通分支数、平均分支角度以及角度标准差共5个指标对不同复杂度的树木骨架在优化前后进行对比分析。其中，节点数反映骨架结构的复杂性和细节保留程度；边数表示骨架中节点之间的连接数量，反映分支的连续性和拓扑完整性；连通分支数通过图论算法统计骨架中互不连通的子图数量，用来衡量骨架的拓扑连通性；平均分支角度通过对每个分叉节点计算相邻边的夹角，取所有角度的平均值。
分支角度标准差($ \sigma $)通过计算所有分支角度的标准差，衡量分支角度的离散程度，其公式如下：
$$ \sigma =\sqrt{\frac{1}{N}\sum _{i=1}^{n}{\left({\theta }_{i}-\bar{\theta }\right)}^{2}} 。$$ (10) 式(10)中：$ n $表示骨架中所有分支角度的总数(即分叉节点的数量)；N表示骨架节点数；$ {\theta }_{i} $ 表示分叉节点的分支角度值；$ \bar{\theta } $ 表示所有分支角度的平均值。
-
由表2可知：相比随机下采样和网格下采样，希尔伯特曲线下采样的点密度保留度表现优异，尤其在保留原始点云的拓扑结构和局部特征方面具有显著优势，计算时间虽然较长，但仍在可接受范围内。针对大规模点云数据处理场景，可通过并行计算(如基于GPU加速)或分块处理策略进一步提升希尔伯特曲线下采样的计算效率。综合来看，希尔伯特曲线下采样的性能优势明显，通过适当优化可满足实际工程应用需求。
表 2 3种点云下采样方法的综合性能分析
Table 2. A comprehensive performance analysis of three point cloud downsampling methods
方法 Hausdorff
距离计算
时间/s点密度
保留度/%下采
样率/%希尔伯特曲线下采样 0.026 5.2 95.73 90 随机下采样 0.134 1.5 72.26 90 网格下采样 0.058 2.3 89.64 90 由图1可以看出：基于希尔伯特曲线的下采样方法在树木点云数据处理中的表现明显优于网格下采样和随机下采样。网格下采样虽然速度较快，但由于采用均匀采样策略，导致点云在树木复杂结构尤其是树冠及细小分支区域的细节丢失，从而影响了模型的精度与完整性。随机下采样通过引入随机性减少了规则性采样带来的缺陷，但缺乏对树木骨架结构的适应性，导致了重要的局部特征被不均匀丢弃，从而影响树木形态的准确再现。相比之下，基于希尔伯特曲线的下采样虽然计算成本较大，但通过自适应的采样策略有效地保留了树木点云的局部几何细节，尤其是在结构复杂和分支密集的区域，能够保持较高的点云密度和细节精度。因此，基于希尔伯特曲线的下采样方法在精度要求较高的树木三维重建任务中表现出更为优越的性能。
图 1 使用希尔伯特曲线、随机和网格下采样算法对点云采样
Figure 1. Downsampled the point cloud using Hilbert curve, random, and grid downsampling algorithms
-
输入下采样后的3株不同种类和复杂度的单株树木点云，采用LeWoS模型进行枝叶分离，结果分别如图2和表3所示。由表3可知：LeWoS 模型在3株木样本上的分类性能整体表现良好。其中，在树1与树2上的总体准确率分别为87.6%和88.4%，F1均超过90%，显示出高精度与稳定性。在树3中，尽管准确率略微下降，但F1仍达87.3%，表明模型在点云结构或特征分布存在差异时仍能保持较好的性能。整体来看，LeWoS模型在木质点识别任务中具有良好的准确性与泛化能力。
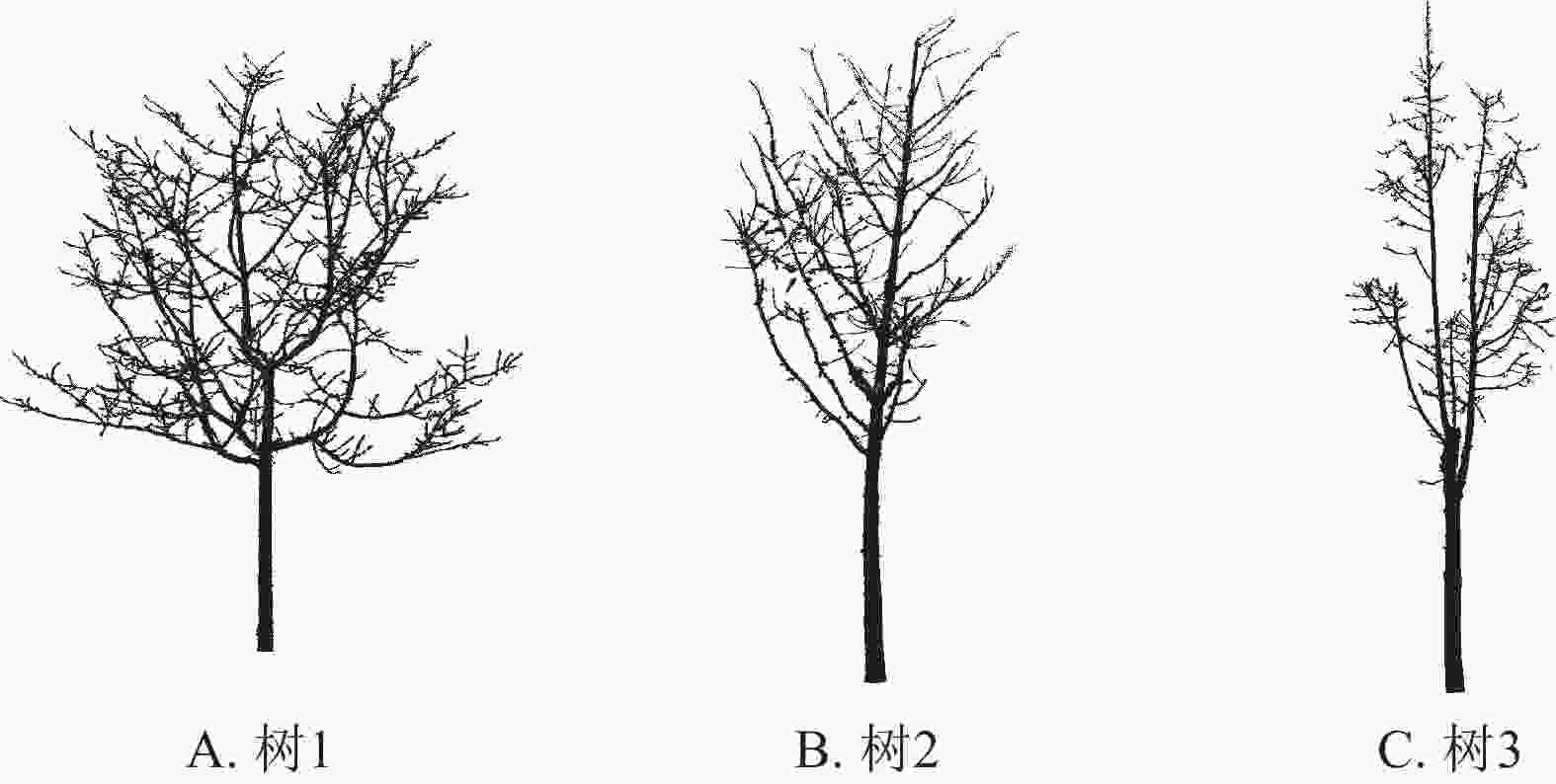
图 2 基于LeWoS模型的3株树木枝叶分离结果
Figure 2. Leaf-wood separation results of three tree species using the LeWoS model
表 3 LeWoS模型在不同树木点云上的分类性能定量评估
Table 3. Performance quantification of the LeWoS model for tree point cloud classification
样本 总体准确率/% 精确率/% 召回率/% F1/% 树1 87.6 91.3 87.4 90.2 树2 88.4 92.2 88.1 90.1 树3 82.9 89.7 85.0 87.3 -
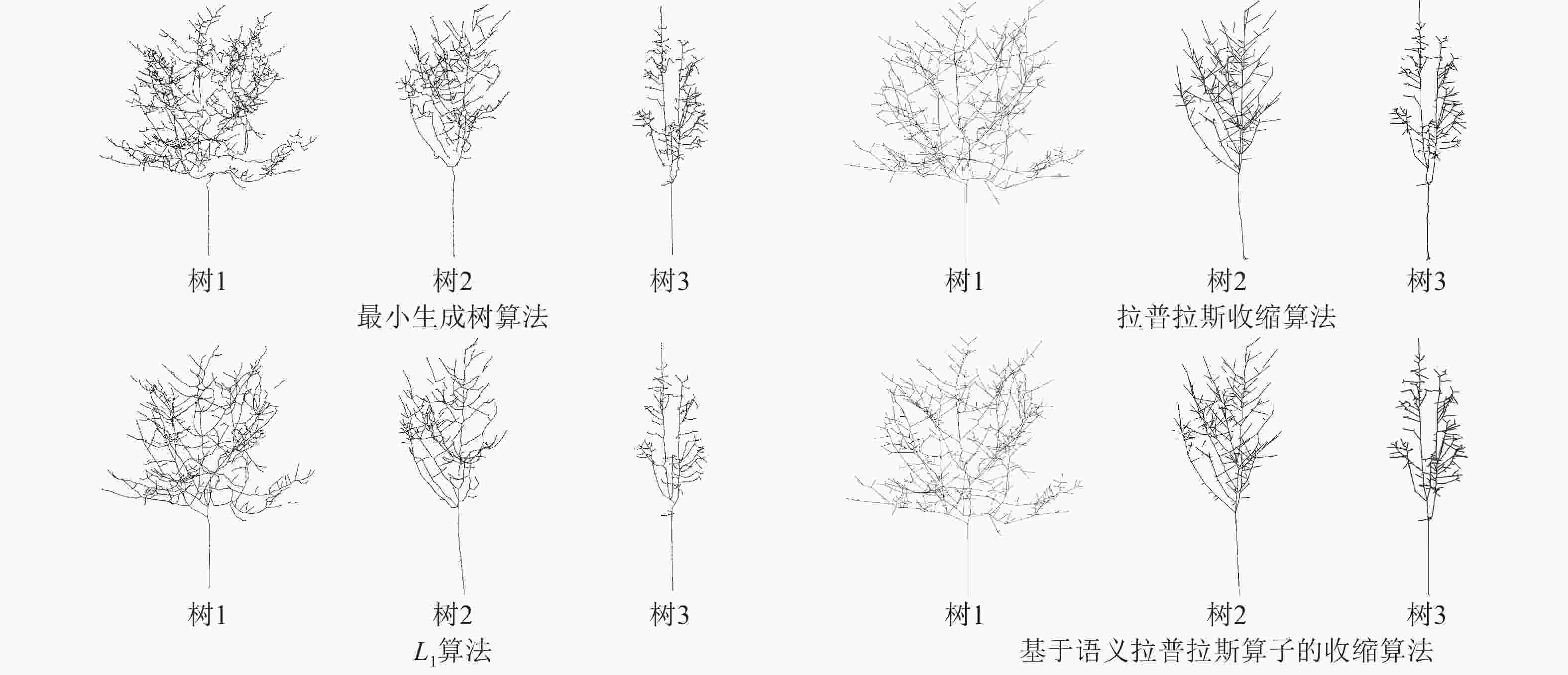
由图3可知：相较于其他3种算法，基于语义拉普拉斯算子的收缩算法能更精确地捕捉树木的几何细节，特别是在枝干和树冠的过渡部分，避免了其他3种算法中出现的断裂和简化现象，表明基于语义拉普拉斯算子的收缩算法通过形状学习技术，能够更好地理解树木的整体形态和细节，提取的骨架更加连贯且细致。
图 3 3株树的初步骨架提取效果
Figure 3. Priliminary skeletons of three tree species
4种骨架提取算法的性能评估结果如表4所示。从骨架节点数量来看，基于语义拉普拉斯算子的收缩算法提取的节点数略多于其他3种算法，表明该方法保留了更多细节，这与图3中观察到的基于语义拉普拉斯算子的收缩算法能更精确捕捉树木几何特征的结果一致。在平均点云间隔方面，基于语义拉普拉斯算子的收缩算法的值比其他3种算法更小，说明其提取的骨架点分布更密集，精度更高，进一步验证了它在枝干和树冠过渡部分的优势。然而，基于语义拉普拉斯算子的收缩算法的运行时间明显长于其他算法，这主要是因为每次迭代均需结合点云的语义类别动态调整收缩权重并重构拉普拉斯矩阵，从而增加了线性系统求解的复杂度。因此，基于语义拉普拉斯算子的收缩算法虽然能更好地保留几何细节，但也带来了更高的计算成本。
表 4 4种算法在树木骨架提取中的性能对比
Table 4. Performance comparison of LBC and S-LBC algorithms in tree skeleton extraction
算法 骨架节点 平均点云间隔/m 运行时间/s 树1 树2 树3 树1 树2 树3 树1 树2 树3 MST 936 507 386 0.018 0.069 0.018 8.98 6.25 10.36 L1 959 523 401 0.015 0.057 0.012 10.59 9.48 11.87 LBC 975 519 418 0.014 0.053 0.019 13.15 10.58 10.67 S-LBC 998 578 470 0.011 0.021 0.013 54.13 51.65 52.15 说明：MST. 最小生成树算法；L1. L1算法；LBC. 拉普拉斯收缩算法；S-LBC. 基于语义拉普拉斯算子收缩算法。 -
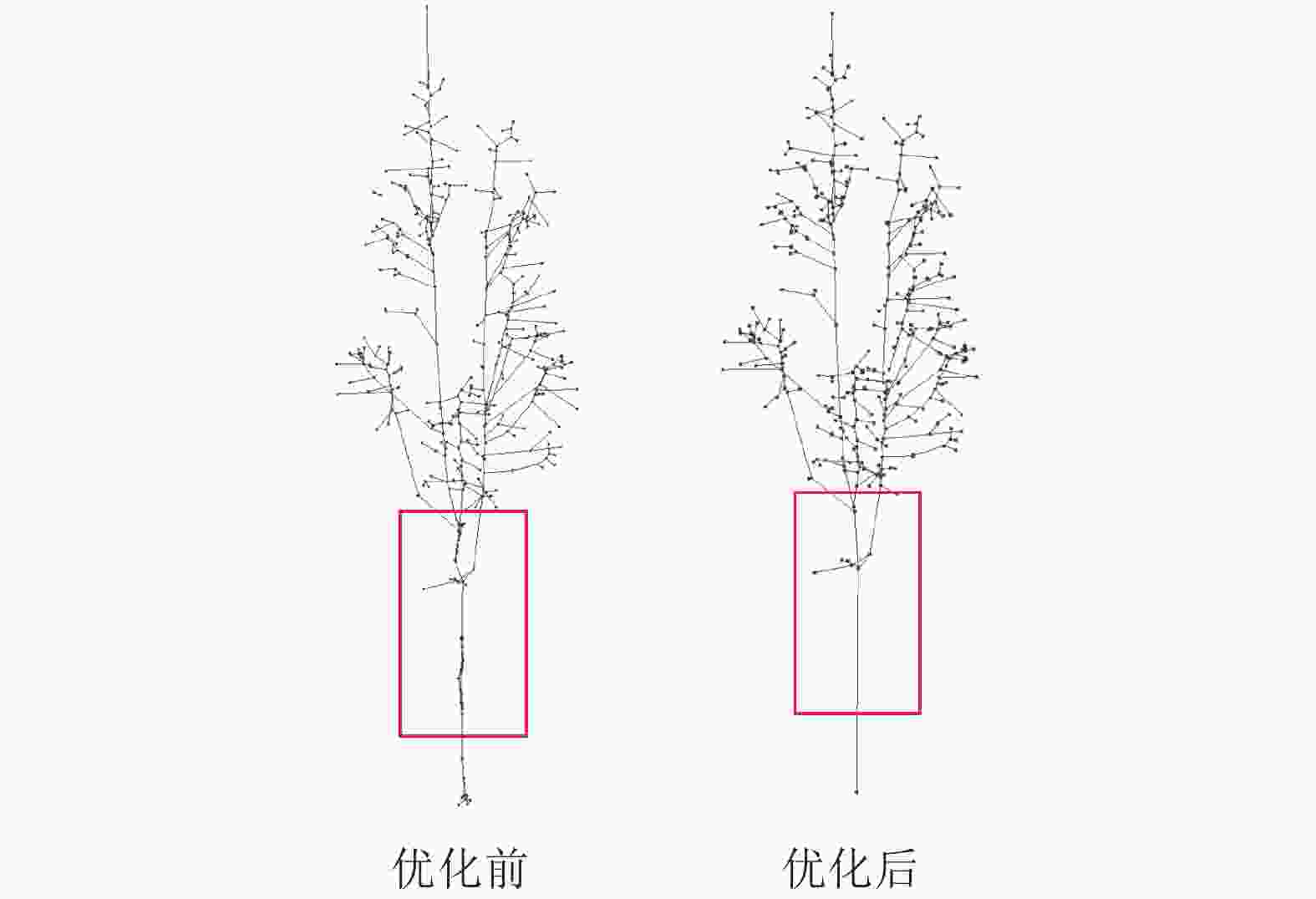
对树木初始骨架进行拉普拉斯平滑处理后的结果如图4所示。优化前骨架存在树干断裂、树枝连接不自然等问题，尤其底部结构较为混乱，影响结构真实性与后续建模精度。经过平滑优化处理后，结构连接更为自然，连续性显著增强，整体形态更贴近真实树木生长特征，几何一致性与生物学解释性得以提升。
图 4 树枝平滑前后对比
Figure 4. Skeleton comparison before and after branch smoothing
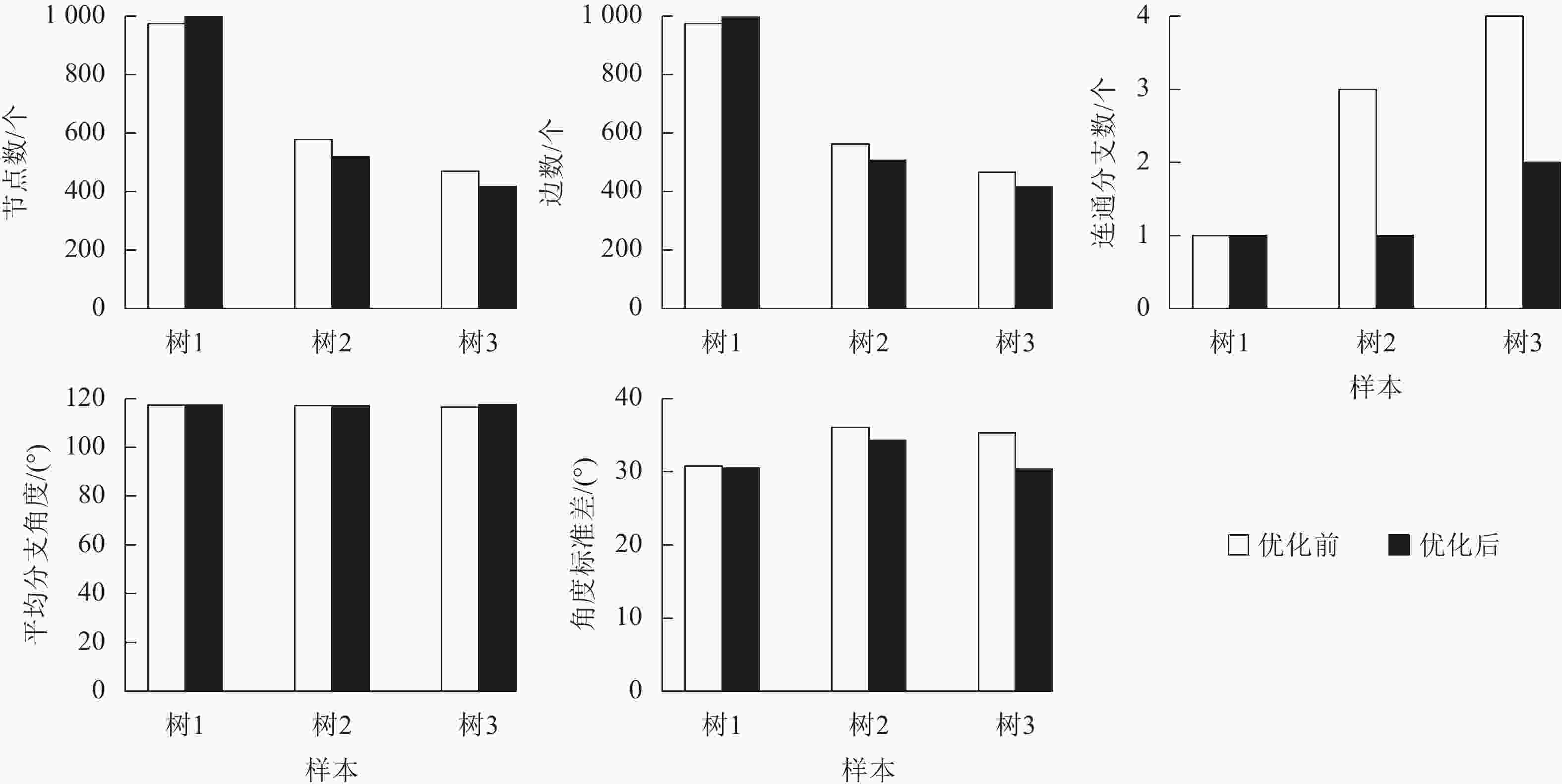
如图5所示：树木骨架在优化后结构参数发生了明显变化。树1在优化后节点数和边数分别增加至998和997个，表明其结构经过补全和连接调整，骨架更加完整。相比之下，树2和树3在优化后节点数分别减少至519和418个，边数也相应减少，说明其原始骨架中存在冗余节点和多余连接，通过优化过程有效地简化了骨架结构。进一步分析连通分支数量可以发现：树2在优化前存在3个分支，优化后减少为1个，树3由4个减少为2个。这表明优化后骨架的连通性明显提升，孤立结构被去除，整体拓扑更加统一。在角度特征方面，3株树的平均分支角度变化不大，始终保持在约117°，说明优化过程保持了枝干的自然生长趋势。从分支角度的标准差来看，3株树均有所下降，这反映出骨架优化提升了分支方向的稳定性，减少了结构中的尖锐折角和异常偏移。综上所述，骨架优化在保证整体结构连贯性的基础上，有效简化了冗余节点与多余连接，同时提升了几何结构的规整性，使优化后的骨架更贴近真实树木的生长形态，为后续三维建模和结构分析提供了更加稳定和可靠的数据基础。
图 5 树木骨架优化前后结构参数的定量对比
Figure 5. Quantitative comparison of structural parameters before and after tree skeleton optimization
-
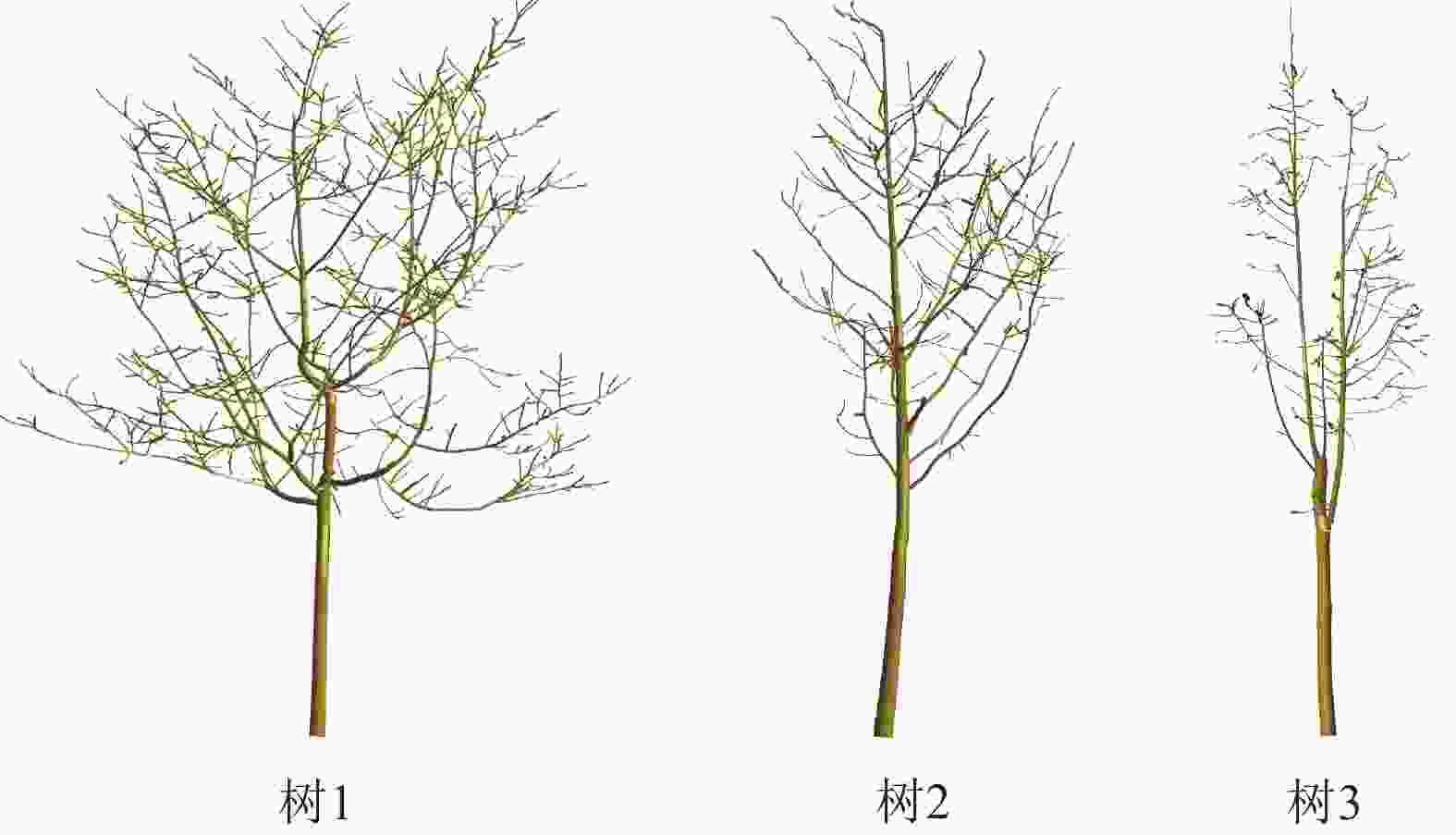
为了验证提取的树木骨架能否准确反映真实树木的形态结构，本研究基于提取的骨架数据对3株树木进行了三维建模，结果如图6所示。从图6可以看出：重建的树木模型完整保留了主干与各级分支的拓扑连接关系，骨架结构层次分明，细小分支的几何特征也得到了良好呈现。此外，各模型的枝干走向自然合理，无明显拓扑错误或结构缺失。上述分析表明：本研究方法提取的骨架具有正确的拓扑结构和良好的几何保真度，能够为后续的树木形态分析和生态参数计算提供可靠的基础数据。
图 6 3株树木的骨架提取结果
Figure 6. Skeleton extraction results of three species of trees
-
为验证本研究提出的方法在不同点云缺失情况下的适应性与鲁棒性，采用随机抽稀重采样算法，分别设置了原始点云的70%、50%和30%，与原始点云(100%)进行对比，模拟不同程度的点云缺失场景。3株树木在4种场景下的建模结果如图7所示。由图7可以看出：即使在高比例点云缺失(30%)的情况下，该方法仍能保持主干和主要分支的拓扑结构完整性，同时通过参数自适应机制有效平衡了几何精度与结构表达的准确性，表明本研究方法对点云缺失情况具有良好的适应能力。
图 7 经过抽稀后的树木点云建模结果
Figure 7. Reconstructed tree models using the different densities of point clouds
-
本研究提出了一种基于地面激光雷达点云的单木骨架提取方法，通过希尔伯特曲线下采样提高计算效率，采用语义拉普拉斯收缩算法提取树木骨架，并结合树枝平滑技术优化骨架结构，有效提升了建模精度和细节保留能力。相比现有方法，在面对结构复杂或点云稀疏的场景常出现骨架断裂、分支简化或拓扑错误等问题，本研究的方法在枝干拓扑保持、细小分支表达及整体结构连续性方面均表现更优，展现出更强的鲁棒性与适应性，可为城市三维建模提供更精准的植被结构数据。
尽管本研究法在三维树木的骨架提取中取得了较为理想的效果，但仍存在一定的局限性。一方面，本研究采用的枝叶分离算法在细小枝条的识别方面精度有限，LeWoS在处理高阶分枝时易将细小枝条误分类为叶片，同时也可能出现将特殊叶片误判为枝条的情况。另一方面，基于语义拉普拉斯算子的收缩算法在面对部分遮挡或局部缺失的点云数据时能够生成较为合理的骨架结构，但当缺失区域较大，尤其是涉及细小枝条时，可能出现拓扑结构还原不完整的情况，影响最终模型的准确性和结构一致性。针对上述问题，未来的研究拟通过改进枝叶分离算法提高对高阶细节结构的识别能力，并进一步增强骨架提取方法在大尺度缺失情况下的鲁棒性与结构恢复能力，以全面提升模型的精度与适用性。
Single tree skeleton extraction algorithm based on terrestrial ground LiDAR point clouds
-
摘要:
目的 提出一种基于地面激光雷达点云的树木骨架提取方法，以实现高精度和高还原度的树木三维重建。 方法 针对分割后的单株树木点云，首先采用希尔伯特曲线进行下采样和降噪处理，以提高计算效率并去除噪声。在完成枝叶分离并获得完整枝干点云后，应用语义拉普拉斯收缩算法提取树木的初始骨架。最后通过树枝平滑技术对骨架进行优化，从而获得高保真、拓扑正确的树木骨架结构。 结果 相比传统方法，该方法提取的骨架节点数平均高12.3%，点云间隔精度平均提升42.0%，达0.011~0.021 m。该方法在拓扑完整性和细节保留方面具有显著优势，同时结合树枝平滑优化技术，进一步增强了骨架的连续性和自然形态。 结论 该方法能够有效克服传统骨架提取算法的局限性，鲁棒性和准确性显著提升，可为植物表型分析、树木长势评估等应用提供高保真的树木骨架数据支撑。图7表4参28 Abstract:Objective This study aims to propose an approach for tree skeleton extraction based on terrestrial LiDAR point clouds, so as to achieve high-precision and high-fidelity 3D tree reconstruction. Method For the segmented point cloud of a single tree, Hilbert curve was used for downsampling and denoising to improve computational efficiency and remove noise. After branch and leaf separation and obtaining the complete branch point cloud, a semantic Laplacian contraction algorithm was applied to extract the initial skeleton of the tree. Finally, the tree skeleton was optimized using branch smoothing technology to obtain a high fidelity and topologically correct tree skeleton structure. Result Compared with traditional methods, the proposed approach extracted an average of 12.3% more skeleton nodes and an average improvement of 42.0% in point cloud interval accuracy, reaching 0.011−0.021 m. This method has significant advantages in topological integrity and detail preservation, while the continuity and natural morphology of the skeleton are further enhanced in combination with the branch smoothing optimization technique. Conclusion This method can effectively overcome the limitations of conventional skeleton extraction algorithms, significantly improve robustness and accuracy, and provide high-fidelity tree skeleton data support for applications such as plant phenotyping and tree growth assessment. [Ch, 7 fig. 4 tab. 28 ref.] -
图 1 使用希尔伯特曲线、随机和网格下采样算法对点云采样
Figure 1 Downsampled the point cloud using Hilbert curve, random, and grid downsampling algorithms
图 2 基于LeWoS模型的3株树木枝叶分离结果
Figure 2 Leaf-wood separation results of three tree species using the LeWoS model
图 5 树木骨架优化前后结构参数的定量对比
Figure 5 Quantitative comparison of structural parameters before and after tree skeleton optimization
图 7 经过抽稀后的树木点云建模结果
Figure 7 Reconstructed tree models using the different densities of point clouds
表 1 Trimble X7仪器参数
Table 1. Detailed parameters of Trimble X7 scanner
指标 参数 指标 参数 扫描EDM激光类别 1类激光，对人眼安全，符合IEC EN60825-1标准 测程 0.6~80.0 m 激光波长 1 550 nm，不可见 高灵敏度模式 暗色(沥青)和反光(不锈钢)表面 视场 360°× 282° 精度验证 具有自动校准，终身保证 扫描时间 最快2 min 34 s(带影像)，1 min 34 s(无影像) 测距精度 2 mm 扫描速度 最大500 kHz 角度精度 21′′ 测量原理 高速、数字飞行时间测距技术 3D点精度 2.4 mm@10 m，3.5 mm@20 m，6.0 mm@40 m 测距噪声 ＜3 mm@60 m，80%反射2 
下载: 导出CSV
表 2 3种点云下采样方法的综合性能分析
Table 2. A comprehensive performance analysis of three point cloud downsampling methods
方法 Hausdorff
距离计算
时间/s点密度
保留度/%下采
样率/%希尔伯特曲线下采样 0.026 5.2 95.73 90 随机下采样 0.134 1.5 72.26 90 网格下采样 0.058 2.3 89.64 90
下载: 导出CSV
表 3 LeWoS模型在不同树木点云上的分类性能定量评估
Table 3. Performance quantification of the LeWoS model for tree point cloud classification
样本 总体准确率/% 精确率/% 召回率/% F1/% 树1 87.6 91.3 87.4 90.2 树2 88.4 92.2 88.1 90.1 树3 82.9 89.7 85.0 87.3
下载: 导出CSV
表 4 4种算法在树木骨架提取中的性能对比
Table 4. Performance comparison of LBC and S-LBC algorithms in tree skeleton extraction
算法 骨架节点 平均点云间隔/m 运行时间/s 树1 树2 树3 树1 树2 树3 树1 树2 树3 MST 936 507 386 0.018 0.069 0.018 8.98 6.25 10.36 L1 959 523 401 0.015 0.057 0.012 10.59 9.48 11.87 LBC 975 519 418 0.014 0.053 0.019 13.15 10.58 10.67 S-LBC 998 578 470 0.011 0.021 0.013 54.13 51.65 52.15 说明：MST. 最小生成树算法；L1. L1算法；LBC. 拉普拉斯收缩算法；S-LBC. 基于语义拉普拉斯算子收缩算法。
下载: 导出CSV
-
[1] KUNZ M, HESS C, RAUMONEN P, et al. Comparison of wood volume estimates of young trees from terrestrial laser scan data [J]. IForest-Biogeosciences and Forestry, 2017, 10(2): 451−458. [2] 夏明鹏, 官凤英, 范少辉, 等. TLS技术在森林资源调查中的应用现状与展望[J]. 西北林学院学报, 2018, 33(3): 238−244. XIA Mingpeng, GUAN Fengying, FAN Shaohui, et al. Application status and prospect of TLS in forest resources inventory [J]. Journal of Northwest Forestry University, 2018, 33(3): 238−244. [3] OVELAND I, HAUGLIN M, GOBAKKEN T, et al. Automatic estimation of tree position and stem diameter using a moving terrestrial laser scanner[J/OL]. Remote Sensing, 2017, 9(4): 350[2025-05-06]. DOI: 10.3390/rs9040350. [4] 许珊珊, 李常春, 张超. 结合背负式激光雷达和无人机机载激光雷达的云南松单木胸径和树高提取[J]. 浙江农林大学学报, 2024, 41(5): 939−948. XU Shanshan, LI Changchun, ZHANG Chao. Extraction of DBH and height of Pinus yunnanensis individual trees by combining backpack laser scanning and unmanned aerial vehicle laser scanning [J]. Journal of Zhejiang A&F University, 2024, 41(5): 939−948. [5] OLSOY P J, MITCHELL J J, LEVIA D F, et al. Estimation of big sagebrush leaf area index with terrestrial laser scanning [J]. Ecological Indicators, 2016, 61: 815−821. [6] KONG Fanhua, YAN Weijiao, ZHENG Guang, et al. Retrieval of three-dimensional tree canopy and shade using terrestrial laser scanning (TLS) data to analyze the cooling effect of vegetation [J]. Agricultural and Forest Meteorology, 2016, 217: 22−34. [7] HAUGLIN M, ASTRUP R, GOBAKKEN T, et al. Estimating single-tree branch biomass of Norway spruce with terrestrial laser scanning using voxel-based and crown dimension features [J]. Scandinavian Journal of Forest Research, 2013, 28(5): 456−469. [8] ZHANG Yuekun, YU Wenjie, ZHAO Xizhi, et al. Interactive tree segmentation and modeling from ALS point clouds[J/OL]. Journal of Graphics, 2021, 42(4)[2025-05-06]. DOI: 10.11996/JG.j.2095-302X.2021040599. [9] 曹伟, 陈动, 史玉峰, 等. 激光雷达点云树木建模研究进展与展望[J]. 武汉大学学报(信息科学版), 2021, 46(2): 203−220. CAO Wei, CHEN Dong, SHI Yufeng, et al. Progress and prospect of LiDAR point clouds to 3D tree models [J]. Geomatics and Information Science of Wuhan University, 2021, 46(2): 203−220. [10] 邓焯, 李斌, 范光鹏, 等. 基于机载激光雷达点云的桉树林分蓄积量估算模型构建[J]. 浙江农林大学学报, 2022, 39(6): 1330−1339. DENG Zhuo, LI Bin, FAN Guangpeng, et al. Estimation model of Eucalyptus stand volume based on airborne LiDAR Point Cloud [J]. Journal of Zhejiang A&F University, 2022, 39(6): 1330−1339. [11] 陶江玥, 刘丽娟, 庞勇, 等. 基于机载激光雷达和高光谱数据的树种识别方法[J]. 浙江农林大学学报, 2018, 35(2): 314−323. TAO Jiangyue, LIU Lijuan, PANG Yong, et al. Automatic identification of tree species based on airborne LiDAR and hyperspectral data [J]. Journal of Zhejiang A&F University, 2018, 35(2): 314−323. [12] 高士增, 张怀清, 刘闽, 等. 树木枝干Delaunay三角网格构建技术[J]. 西南林业大学学报, 2013, 33(3): 62−68. GAO Shizeng, ZHANG Huaiqing, LIU Min, et al. Constructing technology of tree branches delaunay triangulation [J]. Journal of Southwest Forestry University, 2013, 33(3): 62−68. [13] QIN Hongxing, HAN Jia, LI Ning, et al. Mass-driven topology-aware curve skeleton extraction from incomplete point clouds [J]. IEEE Transactions on Visualization and Computer Graphics, 2020, 26(9): 2805−2817. [14] HUANG Zhixian, HUANG Xiao, FAN Jiangchuan, et al. Retrieval of aerodynamic parameters in rubber tree forests based on the computer simulation technique and terrestrial laser scanning data[J/OL]. Remote Sensing, 2020, 12(8): 1318[2025-05-06]. DOI: 10.3390/rs12081318. [15] JIANG Anling, LIU Ji, ZHOU Jianling, et al. Skeleton extraction from point clouds of trees with complex branches via graph contraction [J]. The Visual Computer, 2021, 37(8): 2235−2251. [16] BUCKSCH A, LINDENBERGH R, MENENTI M. SkeITre: Robust skeleton extraction from imperfect point clouds [J]. The Visual Computer: International Journal of Computer Graphics, 2010, 26(10): 1283−1300. [17] FU Lixian, LIU Ji, ZHOU Jianling, et al. Tree skeletonization for raw point cloud exploiting cylindrical shape prior [J]. IEEE Access, 2020, 8: 27327−27341. [18] AI Mingyao, YAO Yuan, HU Qingwu, et al. An automatic tree skeleton extraction approach based on multi-view slicing using terrestrial LiDAR scans data[J/OL]. Remote Sensing, 2020, 12(22): 3824[2025-05-06]. DOI: 10.3390/rs12223824. [19] GAO Linming, ZHANG Dong, LI Nan, et al. Force field driven skeleton extraction method for point cloud trees [J]. Earth Science Informatics, 2019, 12(2): 161−171. [20] JIN Shuangna, ZHANG Wuming, CAI Shangshu, et al. Stem and branch volume estimation using terrestrial laser scanning data [J]. National Remote Sensing Bulletin, 2023, 27(7): 1653−1666. [21] FAN Guangpeng, NAN Liangliang, DONG Yanqi, et al. AdQSM: a new method for estimating above-ground biomass from TLS point clouds[J/OL]. Remote Sensing, 2020, 12(18): 3089[2025-05-06]. DOI: 10.3390/rs12183089. [22] ZHOU Jianling, LIU Ji, ZHANG Min. Curve skeleton extraction via k-nearest-neighbors based contraction [J]. International Journal of Applied Mathematics and Computer Science, 2020, 30(1): 123−132. [23] MENG Cheng, YU Jun, CHEN Yongkai, et al. Smoothing splines approximation using Hilbert curve basis selection [J]. Journal of Computational and Graphical Statistics, 2022, 31(3): 802−812. [24] LI Tao, MENG Cheng, XU Hongteng, et al. Hilbert curve projection distance for distribution comparison [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2024, 46(7): 4993−5007. [25] 李萍, 冯仲科, 苏珏颖. 定量结构模型的地面激光雷达单木分割应用[J]. 测绘科学, 2022, 47(2): 151−156, 199. LI Ping, FENG Zhongke, SU Jueying. Application of quantitative structure model in TLS single wood segmentation [J]. Science of Surveying and Mapping, 2022, 47(2): 151−156, 199. [26] WANG Di, MOMO TAKOUDJOU S, CASELLA E. LeWoS: a universal leaf-wood classification method to facilitate the 3D modelling of large tropical trees using terrestrial LiDAR [J]. Methods in Ecology and Evolution, 2020, 11(3): 376−389. [27] CAO Junjie, TAGLIASACCHI A, OLSON M, et al. Point cloud skeletons via Laplacian-based contraction [C]// PERNOT J P. Proceedings of the 2010 IEEE International Conference on Shape Modeling and Applications (SMI). Los Alamitos: IEEE Computer Society, 2010: 187−197. [28] MEYER L, GILSON A, SCHOLZ O, et al. CherryPicker: semantic skeletonization and topological reconstruction of cherry trees[C]// BROWN M S. Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Los Alamitos: IEEE Computer Society, 2023: 6244−6253. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20250324
点击查看大图
图(7) / 表(4)
计量
- 文章访问数: 552
- HTML全文浏览量: 178
- PDF下载量: 93
- 被引次数: 0
