Age effect on biomass distribution pattern and optimization of allometric growth equation in Eucalyptus urophylla×E. grandis plantations

试验地设置于广东湛江桉树人工林生态系统国家定位观测研究站内(21°16′N，110°05′E)。海拔为80~220 m。根据1980—2020年的长期气象记录，该地属南亚热带海洋性季风气候，年平均降水量为1 760.9 mm，其中77%~85%出现在雨季(5—10月)。年平均气温为23.1 ℃。最低气温为1.4 ℃，出现在1月；最高气温为38.1 ℃，出现在7月，年相对湿度为80.4%^[21]。根据世界土壤资源参考基准，该地区土壤属于由玄武岩风化沉积物发育的暗红湿润铁铝土，土壤呈酸性，0~80 cm土层土壤的平均pH为4.9^[22]。

本研究选取的5个林龄(1、2、3、6和 10 a)的尾巨桉人工林均为平地造林，造林无性系为 DH32-29，造林方式均为挖穴造林，造林密度均为1 666株·hm⁻²。任意2块林分间直线距离均小于1 km，立地差异小，且经营方式完全相同。在每个林龄的尾巨桉人工林中分别建立3个20 m×20 m的正方形样地。对每个样地进行每木检尺，记录胸径(D_BH)和树高(H)，按径阶选取样树，其中1、2年生采用1 cm整化，3年生采用2 cm整化，6、10年生采用3 cm整化 (表1)。整株收割，测量其生物量。

用油锯砍伐尾巨桉样树，测量树高、冠幅、胸径和枝下高。在测定干全长的同时，将干按照2 m规格分成若干木段(在1.3~2.0 m处额外增加1段)，在每个区分段底直径的位置截取圆盘，所余不足2 m长度的干为梢头木，在梢头木底直径的位置也截取圆盘，称取全部木段与圆盘质量，作为干鲜质量。将枝从每个木段上分离，并将叶从枝上完全分离，在原地分别称取枝及叶鲜质量。在1株树中均匀收集圆盘、叶和枝的样本各50 g，送至实验室。

根生物量的测量采用人工挖掘法。首先挖掘树桩，后挖掘其余的根系，并尽可能挖掘至根尖。清理粘附在根上的泥土，并在原地称其鲜质量。称量后收集树桩与根的样本50 g，送至实验室。

将干、枝、叶、树桩和根的样本在恒温干燥箱中以85 ℃烘烤至恒量，计算各部分的含水量。树木各器官干质量均利用含水量由鲜质量换算。地上生物量为干、枝、叶生物量之和；根生物量为树桩与根生物量之和。将其相加得到单株树木总生物量，并计算出各林龄树木不同器官及整株平均生物量。

分别计算每个林龄尾巨桉各器官生物量的平均值、各器官生物量占总生物量的百分比，及根生物量与地上部分生物量、叶生物量与干生物量、枝生物量与干生物量的比值，并研究其变化与林龄变化之间关系。绘制树木各器官生物量与地上部分生物量的关系。

本研究参考XIANG等^[23]的异速生长模型，将所有变量经过自然对数转换后(确保各变量之间的线性关系并使其满足异方差的要求)，采用单独的胸径 (D_BH)、单独的树高(H)、胸径和树高的组合(D_BH ² H)，以及胸径(D_BH)和树高(H)同时作为预测变量4种模型形式来建立不包含林龄的各器官异速生长模型1~24。另外，又将林龄作为补充变量引入上述4种模型形式，同时考虑林龄的个体效应及其与其他预测变量(即D_BH、H和D_BH ² H)间的交互效应，建立包含林龄的各器官异速生长模型25~48，以验证引入林龄是否可以提升模型对生物量预测的准确性。

在以前的研究中，只有使用最广泛的2个方程，即D_BH模型和D_BH ² H模型有加入林龄的拟合研究。在本研究中则对上述所有方程均加入了林龄作为拟合变量，且同时选取每个树木器官的包含了林龄的最佳拟合方程。另外，由于对生物量进行对数转换会对回归估计带来偏差，因此，将用于预测的模型反向转换时需要计算矫正因子(F_C)进行偏差矫正^[11]。

本研究采用R-3.6.3的nlme包对模型进行拟合，并估计截距、斜率和树木各器官生物量与预测变量的固定效应之间的关系。

对于拟合的结果，计算赤池信息准则(C_AI)^[24]和残差标准误(E_RS)，以确定模型的适用性。同时，为了比较各模型的拟合优度，随机选取70%的数据进行模型拟合，另外30%用于验证模型拟合能力。将验证集中使用模型计算的预测值与树木生物量的实测值进行对比，利用调整决定系数($ {{R}}_{\text{adj}}^{\text{2}} $)和平均预测误差(E_MP)估计模型拟合优度。

本研究利用R-3.6.3进行数据分析，利用Origin 2022绘图。

由图1A可知：尾巨桉各器官平均单株生物量随林龄增长而增加，其中干生物量由1年生的2.62 kg·株⁻¹增长至10年生的206.67 kg·株⁻¹；枝生物量由1年生的1.13 kg·株⁻¹增长至10年生的31.81 kg·株⁻¹；叶生物量由1年生的0.95 kg·株⁻¹增加至10年生的8.81 kg·株⁻¹；根生物量由1年生的1.10 kg·株⁻¹增加至10年生的55.52 kg·株⁻¹。在所有林龄中，干生物量均最大，其在总生物量中的占比随林龄增加而增加，从1年生的45.21%增加至10年生的68.25%，叶生物量及枝生物量均随林龄的增加而呈下降趋势，其中叶生物量占比由1年生的16.31%下降至10年生的2.91%，枝生物量占比由1年生的19.43%下降至10年生的10.51%。根生物量随年龄的变化则呈相对稳定趋势，自19.05%上升至25.21%后，又回落至18.33%(图1B)。

Figure 1.  Patterns of biomass allocation in E. urophylla×E. grandis at different stand ages

各器官生物量与地上生物量呈现出显著的线性关系(图2)，其中干生物量的回归斜率最高，为0.849，决定系数(R²)为0.998；叶生物量的回归斜率最低，为0.030，R²为0.900；枝和根生物量的回归斜率分别为0.121和0.208，R²分别为0.923和0.884。这说明随着地上生物量的增加，各器官生物量的增长率不同，从大到小依次为干、根、枝、叶。由表2可见：根生物量与地上生物量的比值(根冠比)在各林龄间的平均值由0.235增加至0.337，后下降至0.225，总体趋势平稳。多重比较后发现：1、2、6、10年生林龄间根冠比数值无显著差异，所有林龄根冠比平均值为0.26。枝生物量与干生物量的比在2年生之前下降，此后维持在0.14左右。叶生物量与干生物量比在1~2年生时急剧下降，由0.361降至0.107，在3~10年生时略微下降(0.043~0.068)。

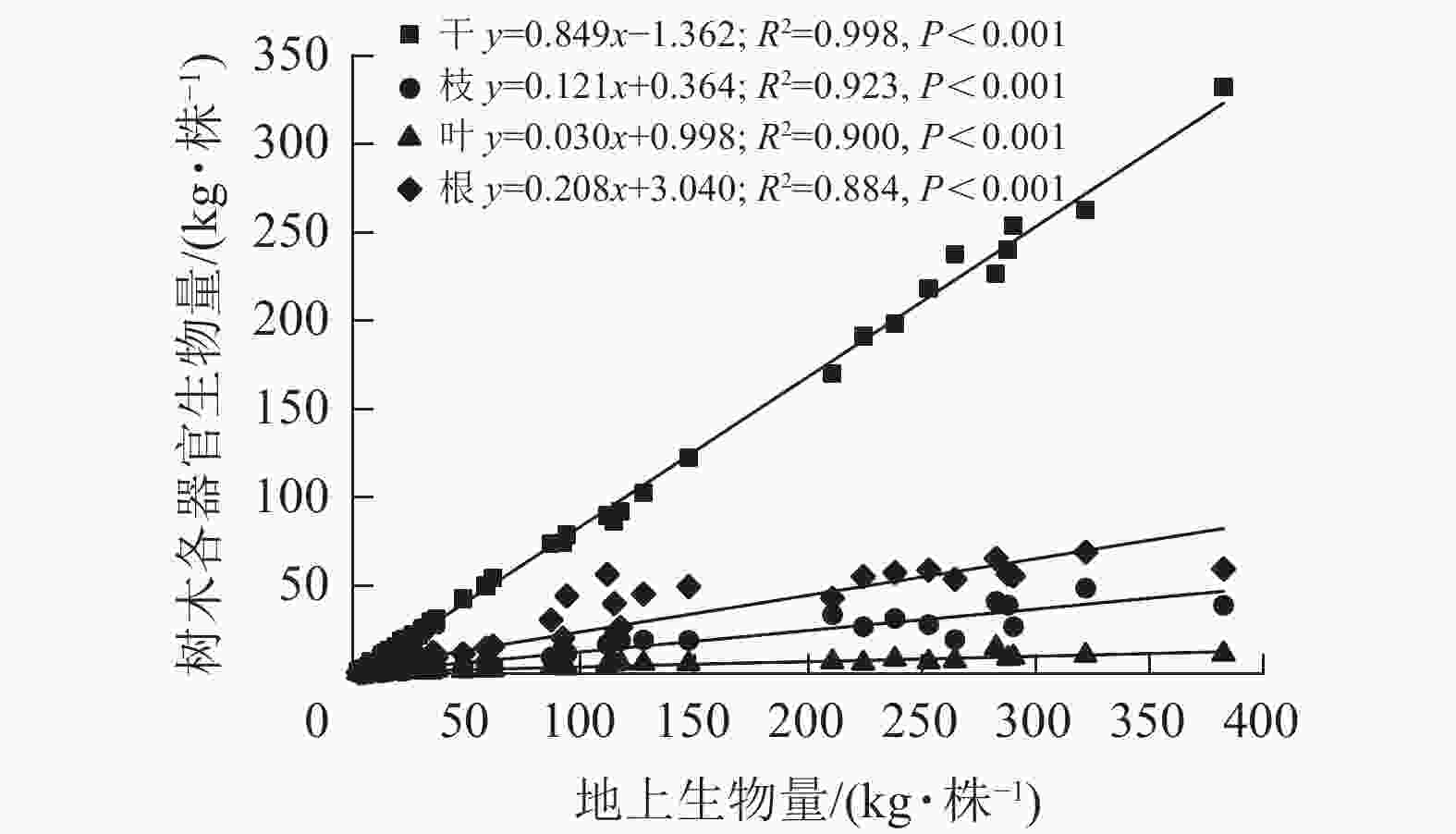
Figure 2.  Fitting of individual tree biomass of various organs of E. urophylla×E. grandis with aboveground biomass

对尾巨桉各器官(根、枝、干、叶)，地上生物量及总生物量进行回归分析，共建立24个不含林龄的尾巨桉生物量异速生长模型(表3)。依据$ {{R}}_{\text{adj}}^{\text{2}} $、E_MP和C_AI对模型拟合效果进行评价。评价结果表明：干生物量最优模型为模型4 (D_BH和H模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.992， E_MP=6.532%；枝生物量最优模型为模型8 (D_BH和H模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.880， E_MP=4.654%；叶生物量最佳模型为模型12 (D_BH和H模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.684， E_MP=3.131%；根生物量最优模型为模型13 (D_BH模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.961， E_MP=5.702%。对地上生物量和总生物量的拟合发现，无最大$ {{R}}_{\text{adj}}^{\text{2}} $和最小E_MP的组合，因此引入C_AI作为辅助评价指标。选取地上生物量各模型中具有最大${{R}}_{\text{adj}}^{\text{2}} $的模型17和具有最小E_MP的模型20，并选取C_AI最小的模型。对总生物量各模型采用相同选择方式，在模型21和模型24中，选取C_AI最小的模型，即地上生物量最优拟合模型为模型17 (D_BH模型)，总生物量最优拟合模型为模型21 (D_BH模型)。

将林龄作为自变量加入后再次进行回归分析，建立了加入林龄自变量的生物量异速生长模型共24个(表4)，其中树干生物量最优模型为模型27(D_BH和H+林龄模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.993，E_MP=7.167%；枝生物量最优模型为模型32 (D_BH和H+林龄模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.894，E_MP=3.931%；根生物量最优模型为模型37 (D_BH+林龄模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.959，E_MP=7.164%；叶生物量、地上生物量及总生物量无最大$ {{R}}_{\text{adj}}^{\text{2}} $和最小E_MP的组合。对于叶生物量，仅有模型35的$ {{R}}_{\text{adj}}^{\text{2}} $在0.9以上，因此可认为模型35为最佳模型(D_BH ² H+林龄模型)。对于地上生物量和总生物量，和不含林龄的异速生长模型选取的方式相同，于模型43、模型44和模型47、模型48中分别选取C_AI最低拟合方程，得出地上生物量最优模型为模型43 (D_BH ² H+林龄模型)，总生物量最优模型为模型47 (D_BH ² H+林龄模型)。

将不含林龄的各器官异速生长方程和加入林龄的各器官异速生长方程对比。在干水平上，不含林龄的异速生长方程最优模型为模型4，加入林龄后的异速生长方程最优模型为模型27。将两者进行比较，模型4的$ {{R}}_{\text{adj}}^{\text{2}} $小于模型27，模型27的E_MP大于模型4，且两者$ {{R}}_{\text{adj}}^{\text{2}} $均大于0.99，将两者的预测值进行t检验，结果无显著差异(P=0.978)。由此可知：在干生物量预测方面，模型4与模型27均可视为最佳预测模型。在枝水平上，不含林龄的异速生长方程最优模型为模型8，加入林龄的最优异速生长模型为模型32，比较发现模型32的$ {{R}}_{\text{adj}}^{\text{2}} $大于模型8，且E_MP小于模型8。由此可知：在枝水平上，加入林龄的模型32为最优预测模型。在叶生物量的8个模型中，仅有加入林龄的模型35的$ {{R}}_{\text{adj}}^{\text{2}} $＞0.9，因此选择模型35为叶生物量预测的最佳模型。在根水平上，不含林龄的最优模型(模型13)拥有比加入林龄的最优模型(模型37)更大的$ {{R}}_{\text{adj}}^{\text{2}} $与更小的E_MP。由此可知：根生物量的最佳预测模型为不含林龄的模型13。在地上生物量水平上，比较不含林龄的最佳模型(模型17)与加入林龄的最佳模型(模型43)，发现模型43为两者中具有较的大$ {{R}}_{\text{adj}}^{\text{2}} $和较小的E_MP，因此模型43为地上生物量的最佳预测模型。在全株生物量水平上进行比较，不含林龄最优模型21的E_MP=17.691%，小于加入林龄最优模型47 (E_MP=19.751%)。由此可知：在全株生物量预测中，不含林龄的模型21为最优模型。

林龄对树木生物量分配格局的影响既是树木自身生长的结果，同时也是树木为保证各个器官的生理活动和功能而进行资源分配平衡的结果^[25−26]。以前的研究表明：植株的地上生物量在总生物量中的占比为79.00%^[27−28]。本研究发现：尾巨桉人工林的地上生物量占总生物量的比例为74.79%~81.67%。地上生物量随林龄变化的分配模式为随着林龄的增长，干生物量占比逐渐增加，而枝生物量与叶生物量的占比逐渐减小。这与很多研究的结论相似^[29−33]。在幼龄期，较高的枝和叶生物量占比，可以保证更多的生物量被分配用于光合作用^[21]，这对于幼树的存活极为重要^{[30, 34]}。随着林龄的增长，树木为了保证自身的物理稳定性^[30]，会将更多的生物量分配给干的生长，因此叶和枝生物量增加的比例小于干生物量增加的比例^[25]，进而导致干生物量占比随林龄逐渐增大，而枝和叶生物量占比随林龄的增大逐渐减小。根生物量在总生物量中的占比随林龄变化无一定规律。在本研究中，根生物量占比先增加，后逐渐下降，直至稳定，为18.33%~25.21%。这与其他研究得出的根生物量占比在林分建立后即大幅下降，最终稳定在一个数值的结论并不一致^{[30, 35]}。这可能是由于人工林的人为抚育措施，尤其是施肥，对根系发育有着重要的影响，施肥时间的不固定性同样会导致根系生物量所占比例发生起伏^[19]。

本研究发现：与对其他树种的研究结果一致^{[7, 36−40]}，尾巨桉各器官生物量均符合异速关系理论；加入树高变量后，除根生物量、地上生物量及总生物量以外，其余各器官生物量的异速生长方程拟合效果均有提升。有许多研究也讨论了树高作为第2变量加入后对树木生物量异速生长方程的影响^[41−43]，如WANGER等^[41]对白松Pinus armandii进行研究，发现树高的加入改善了叶生物量异速生长方程的预测精度，XIANG等^[23]对杉木Cunninghamia lanceolata的研究表明：加入树高变量后，提高了干、枝及叶生物量模型的预测精度；CIENCALA等^[43]研究认为：赤松Pinus densiflora树高的加入轻微改善了各器官生物量方程的拟合效果。但JENKINS等^[44]在对美国主要树种进行异速生长方程研究后认为：树高并不是一个有效变量，仅小部分改善预测效果。

林龄的加入对树木不同器官生物量的预测模型的改善程度并不相同。当将林龄加入异速生长方程后，枝、叶和地上生物量的异速生长方程的拟合效果均有改善，其中叶生物量方程的拟合效果改善最为明显，但对干生物量、根生物量和总生物量的拟合效果改善不大。这与PEICHL等^[30]对白松的年龄序列下各器官生物量异速生长方程的研究结果一致。他们的研究表明：林龄变量的加入可改善枝和叶生物量的估算。XIANG等^[23]对杉木的研究也表明：枝、叶生物量在不同林龄中有较高的变异。SAINT-ANDRÉ等^[29]对杂交桉E. hybrid的研究也发现：林龄的加入改善了干、枝、叶和地上生物量的预测效果，但未改善根生物量的预测效果。同时他们也指出：加入林龄后，预测结果的变异不是林龄单一作用的结果，而是林龄和竞争共同作用的结果。BOND-LAMBERTY等^[45]在研究6种北方树种的地上和地下生物量异速生长模型时引入了林龄，但发现引入林龄后对预测效果的改善并不总是具有显著性，具体取决于立地条件和树种。因此，在建立异速生长模型时，除考虑常规测树因子(树高、胸径、林龄等)以外，还需考虑竞争关系和立地条件等因素。

尾巨桉人工林各器官的生物量分配格局存在明显的林龄效应。随着尾巨桉林林龄的增加，枝、叶生物量占总生物量的比例逐渐下降，而干生物量占总生物量的比例逐渐增加，根生物量的比例先增加后下降，整体呈稳定趋势。在异速生长模型拟合效果对比中，加入树高因素后，干生物量、枝生物量及叶生物量模型的预测效果明显改善，但对根生物量、地上生物量及整株生物量预测效果的影响较小。将林龄作为变量加入异速生长方程后，枝生物量、叶生物量和地上生物量方程的预测结果明显改善，而对根生物量、干生物量及整株生物量影响较小。在各器官生物量最优模型选择上，以单独的D_BH为自变量的模型对根生物量和总生物量的预测要优于其他模型；以D_BH ² H+林龄为自变量的模型对叶生物量和地上生物量的预测最佳；以D_BH和H+林龄为自变量的模型对枝生物量的预测最佳；在对干生物量的预测精度对比中，以D_BH和H与以D_BH ² H+林龄为自变量的预测模型之间无显著差异，均能较好的预测干生物量。