下载:
-
树种结构指森林中树种的组成、数量及彼此之间的关系[1]，是反映森林结构与功能关系的重要内容之一。树种组成是树种结构中最为重要的内容，是构成树种结构的基础。树种组成多样性反映了林分中树种构成的复杂程度和对光热水等自然资源的均衡利用程度，以及固碳释氧、生物种质资源保存等功能的有效性，具有重要生态学意义。树种组成信息丰富，为尽可能全面表达，往往需要使用详尽的语言或借助表格形式进行呈现[2-5]，根据各树种蓄积量所占比例表示树种组成式，满足了人们对树种组成概要描述的需求，但不适用于森林多样性、精准经营、定量分析、对比评价和数字化管理等工作。汤孟平等[6]引入了Shannon物种多样性指数，提出了树种组成指数，并将树种组成式进行数量化。树种组成指数值与树种组成式的系数构成一一对应关系，间接体现了主要树种间的蓄积比例，但未涵盖稀疏树种、树种株数及其分布等信息。可见，树种组成指数值用于定量化表征树种组成多样性是不够全面的。
目前，对于树种组成多样性的定量表述，往往借助于α多样性指数，但依旧存在局限性。王寿兵[7]和赵中华等[8]研究发现：多样性指数本身存在不足与缺陷，一般的多样性指数无法全面客观地反映林分树种组成的重要林学属性。如何科学定量化表达林分树种组成，构建数量化指标的问题值得深入研究[9]。鉴于此，本研究对树种组成多样性的数量化方法进行了探究，构建了树种组成多样性指数，以期为树种组成的表征提供新的度量角度与多样性评价方法，为森林质量评价、森林结构优化调控和森林质量精准提升提供理论和技术依据。
-
林分树种组成多样性指数构建既要遵循生物多样性表征的基本规律和要求，又要充分体现林分树种组成的具体特征和经营管理要求。满足树种丰富度越大，树种分布越均匀，指数值就越高这一基本思想。
树种组成多样性指数的构建首先应满足生物多样性意义，指数值应分别与树种丰富度、分布均匀度呈相应的正向等比关系。其次，应以科学合理的方式结合丰富度、均匀度等多方面信息。最后构建的指数值体现相应的树种组成特征，反映树种总数、树种密度以及树种蓄积(生物量)比例和分布等多方面的内在相关信息。
构建指数选用指标时应兼顾科学性和可操作性2条重要原则[10]。科学性主要从指标的构建方法考虑，涉及构建的指标参数应当准确客观，具有指征性、代表性和可比性。参数之间应相互补充、相对独立，尽可能全面而不重复地反映树种组成特征。可操作性体现在计算指标的原始数据要容易收集，指标计算方法不宜太复杂，要容易被理解接受并易于推广使用等。
-
基于树种组成多样性指数构建的基本理论和要求，对体现树种丰富度的信息与各树种均匀度的信息进行分解使其相对独立，并通过和式进行综合。用树种数体现树种丰富度的信息，用现实林分各个树种的实际株数、蓄积比例与理想林分中完全均匀分布时的树种株数、蓄积所占比例值(1/s，s为树种数)进行较差，并赋予树种株数均匀度、蓄积均匀度相同的权重关系，用平方消除正负值偏差，以体现各树种均匀度的信息，并使之与丰富度信息之间不产生交互和干扰作用。构建的林分树种组成多样性指数(ISCD)计算模型为：
$$ {I_{{\text{SCD}}}} = s - \frac{1}{2}\sum\limits_{i = 1}^s {\left[ {{{\left( {\frac{{{v_i}}}{v} - \frac{1}{s}} \right)}^2} + {{\left( {\frac{{{n_i}}}{n} - \frac{1}{s}} \right)}^2}} \right]} 。 $$ (1) 式(1)中：ISCD为树种组成多样性指数；s为树种数；v为森林总蓄积量；vi为森林中树种i的蓄积量；n为森林总株数；ni为森林中树种i的株数。
-
ISCD与树种数、树种株数和树种蓄积比例分布均匀性呈正相关。作为正向指标，ISCD直接体现林分树种组成多样性的特征，并具有以下意义：①ISCD表达了林分中树种数这一重要特征。绝对纯林时，树种数s为1，ISCD为1。非绝对纯林时，树种数s≥2，ISCD为(s−1，s]，林分的丰富度或树种数可由ISCD向上取整得到，即可以根据数值所处范围直接确定树种数。当林分中树种数相等时，树种混交程度越高，各树种的株树、蓄积分布越均匀，其比例越接近于1/s，则ISCD越大；当林分中所有树种在株数和蓄积2个方面都呈均匀分布时，ISCD达到最大值s。②ISCD表达了林分中各树种的株数、蓄积比例及分布均匀性，体现出混交程度。林分树种均匀度、混交度由ISCD值的小数部分体现。当林分中树种间均匀度、混交度越小，ISCD值的小数部分就越小；反之就越大。小数部分与数值1的差值体现在一定树种数下，实际林分与分布最均匀、混交度最高时的理想林分之间的差异程度。由于同时考虑了不同树种的株数占比和蓄积占比，ISCD更能全面反映树种的分布及混交情况。
-
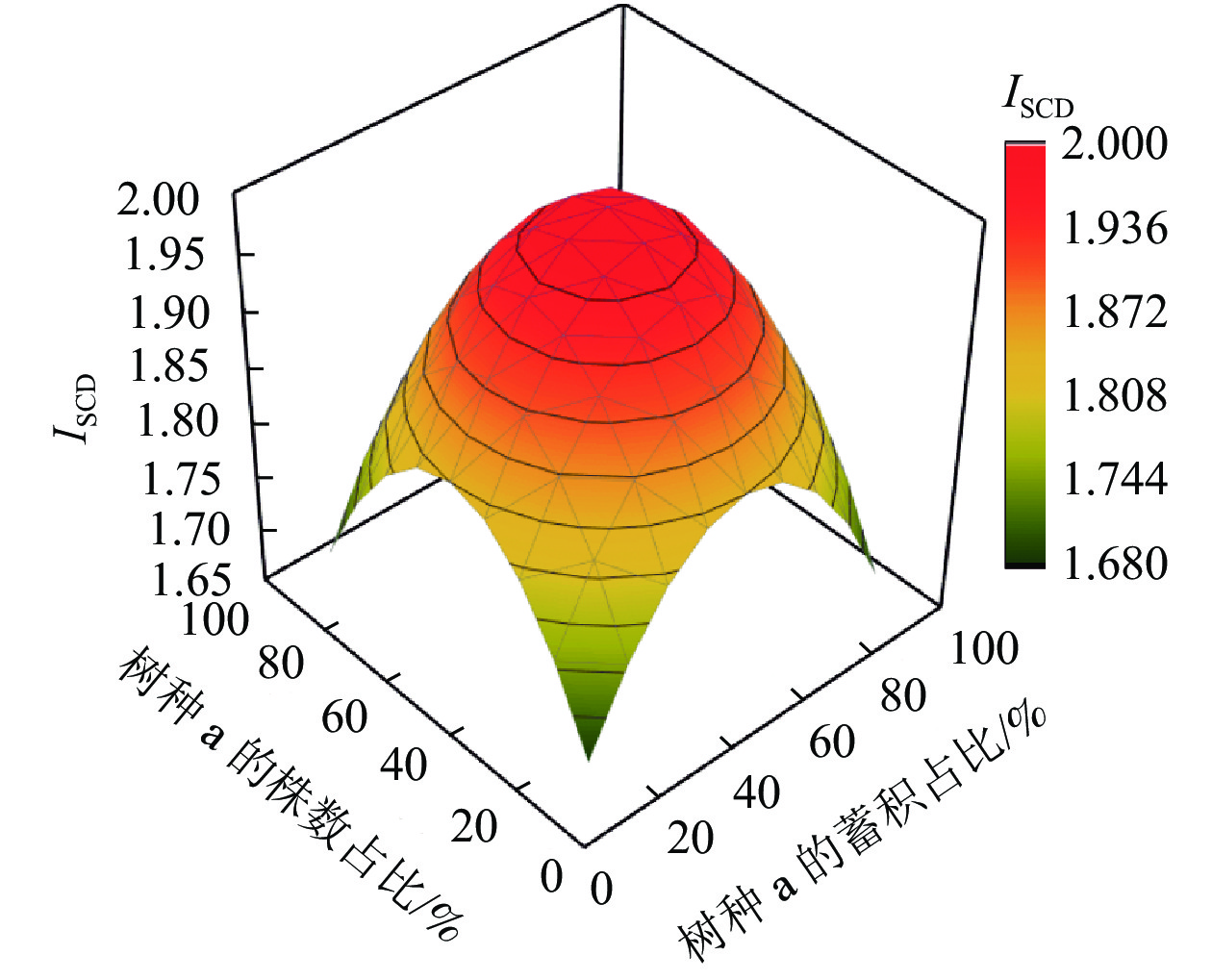
从图1可以看出：当2个树种的株数、蓄积比例分布越不均匀，即某个树种的株数、蓄积占比越接近100%，另一个树种的株数、蓄积占比越接近0时，ISCD就越小，其值就越接近于s−1；当2个树种的株数、蓄积分布越平均，即占比各自越接近50%时，树种结构多样性指数就越趋近最大值2。
图 1 树种数为2个时的树种组成多样性指数(ISCD)变化趋势
Figure 1. Trend of diversity index of tree species composition (ISCD) for two species
-
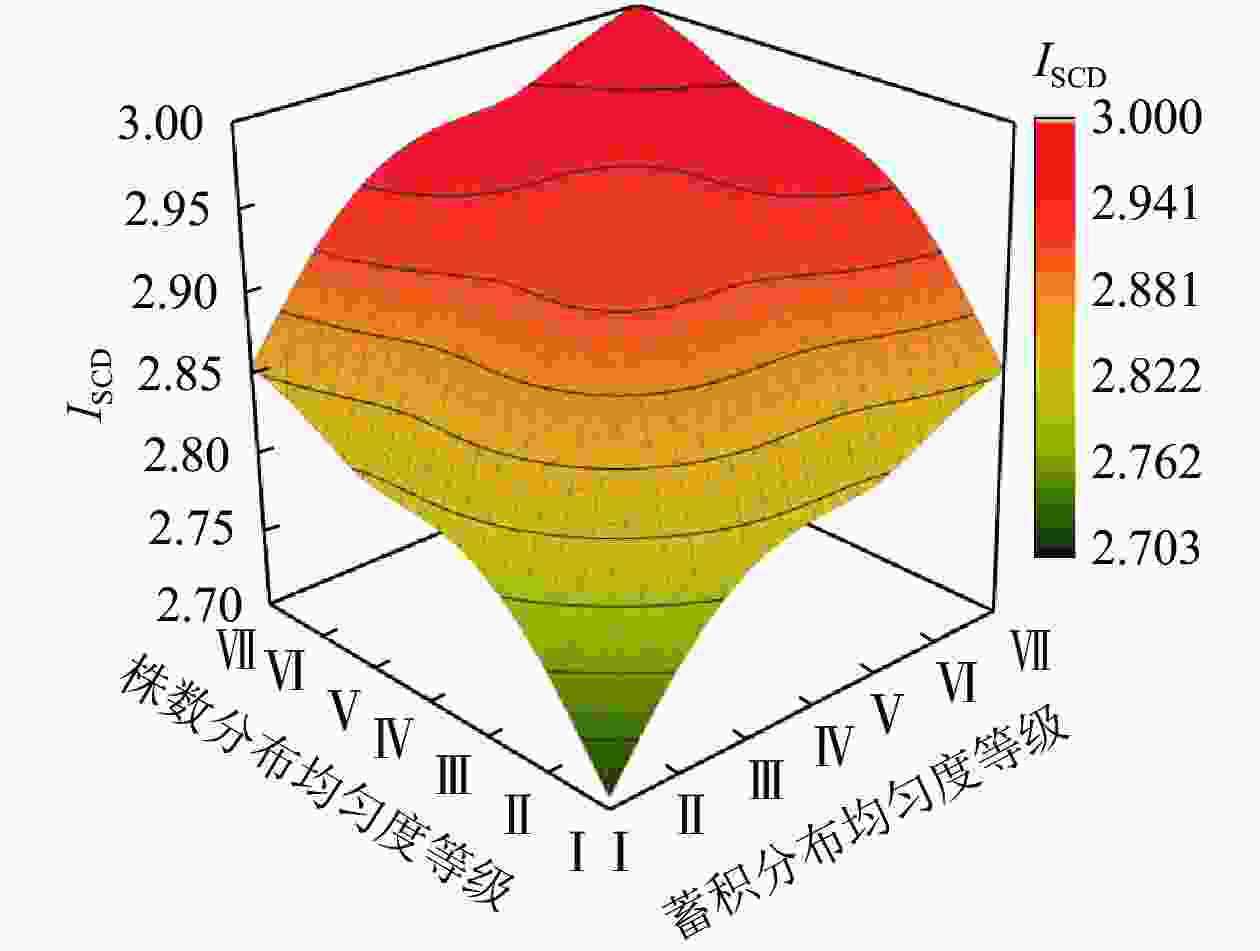
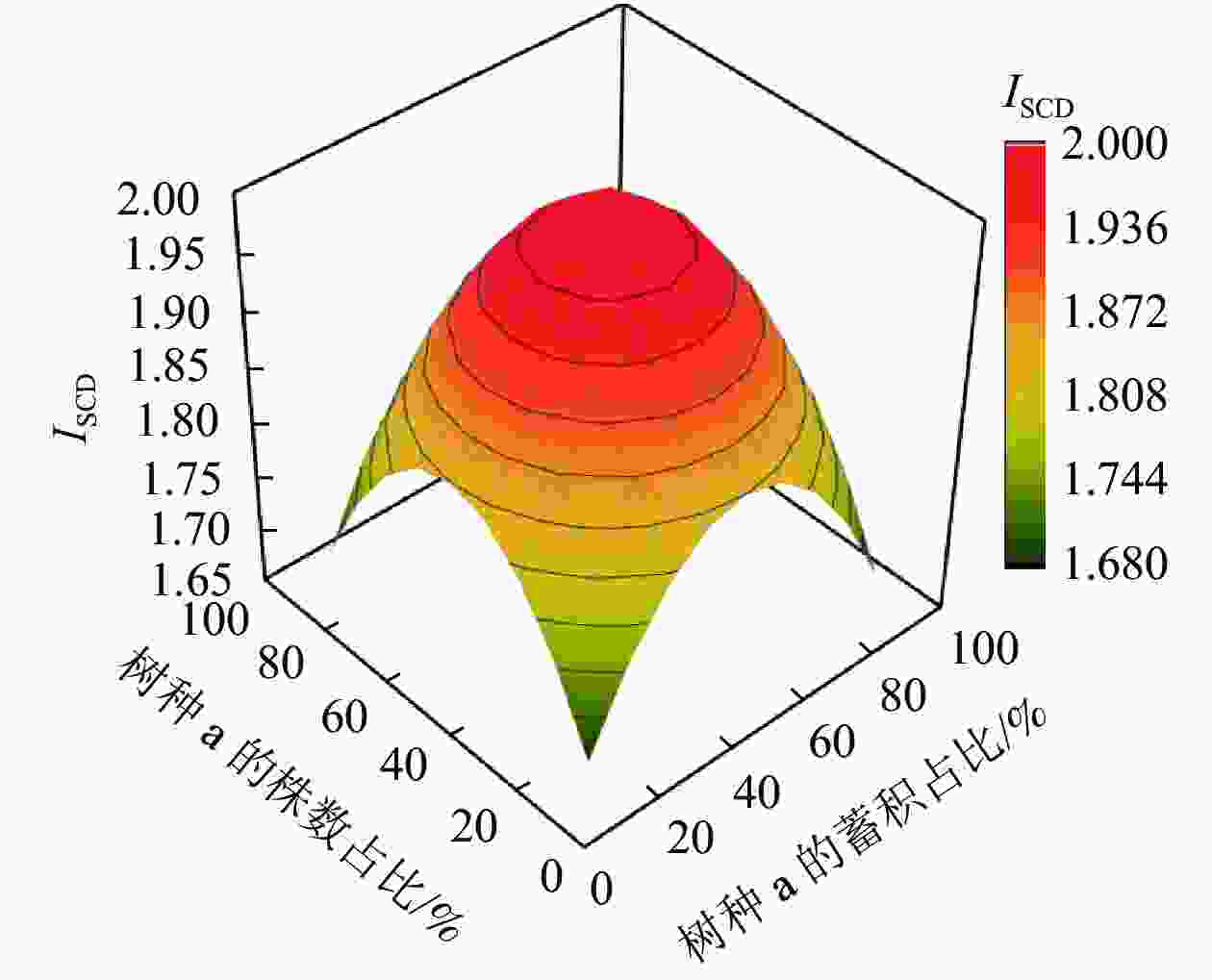
当树种数大于2个时，将各树种的株数和蓄积比例按照其分布均匀程度，进行相应的等级(状态)划分，并以此作为x轴、y轴和z轴数据。设当树种数为3个时，对树种a、b、c存在的株数(或蓄积)分布等级按“3等份”进行划分，并根据Simpson均匀度指数进行分级，株数(或蓄积)分布等级见表1。其中，均匀度等级越大，表明株数(或蓄积)分布的均匀程度越高，Ⅶ为最理想的完全均匀状态。根据表1，对树种的均匀性分布类型组合进行汇总，得到表2。对现实林分中不同均匀度等级之间还存在的连续过渡类型，拟合ISCD变化趋势曲面图(图2)表明：森林中各树种的株数与蓄积的分布均匀度等级越高，ISCD越大，越接近最大值3。与树种数为2个时的规律一致，株数和蓄积分布不均都会导致最终的指数值远小于最大值，ISCD越接近于s−1。
表 1 树种数为3个时的株数(或蓄积)分布均匀度等级
Table 1. Distribution uniformity grade of plants number (or volume) of 3 tree species
分布均匀
度等级树种a
占比树种b
占比树种c
占比Simpson均匀
度指数Ⅰ 1/9 1/9 7/9 0.622 Ⅱ 1/9 2/9 6/9 0.773 Ⅲ 1/9 3/9 5/9 0.853 Ⅳ 1/9 4/9 4/9 0.879 Ⅴ 2/9 2/9 5/9 0.906 Ⅵ 2/9 3/9 4/9 0.966 Ⅶ 3/9 3/9 3/9 1.000 表 2 树种均匀性分布类型
Table 2. Summary of tree species uniformity distribution types
树种株数分布
均匀度等级树种蓄积分布均匀度等级 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅰ (Ⅰ，Ⅰ) (Ⅰ，Ⅱ) (Ⅰ，Ⅲ) (Ⅰ，Ⅳ) (Ⅰ，Ⅴ) (Ⅰ，Ⅵ) (Ⅰ，Ⅶ) Ⅱ (Ⅱ，Ⅰ) (Ⅱ，Ⅱ) (Ⅱ，Ⅲ) (Ⅱ，Ⅳ) (Ⅱ，Ⅴ) (Ⅱ，Ⅵ) (Ⅱ，Ⅶ) Ⅲ (Ⅲ，Ⅰ) (Ⅲ，Ⅱ) (Ⅲ，Ⅲ) (Ⅲ，Ⅳ) (Ⅲ，Ⅴ) (Ⅲ，Ⅵ) (Ⅲ，Ⅶ) Ⅳ (Ⅳ，Ⅰ) (Ⅳ，Ⅱ) (Ⅳ，Ⅲ) (Ⅳ，Ⅳ) (Ⅳ，Ⅴ) (Ⅳ，Ⅵ) (Ⅳ，Ⅶ) Ⅴ (Ⅴ，Ⅰ) (Ⅴ，Ⅱ) (Ⅴ，Ⅲ) (Ⅴ，Ⅳ) (Ⅴ，Ⅴ) (Ⅴ，Ⅵ) (Ⅴ，Ⅶ) Ⅵ (Ⅵ，Ⅰ) (Ⅵ，Ⅱ) (Ⅵ，Ⅲ) (Ⅵ，Ⅳ) (Ⅵ，Ⅴ) (Ⅵ，Ⅵ) (Ⅵ，Ⅶ) Ⅶ (Ⅶ，Ⅰ) (Ⅶ，Ⅱ) (Ⅶ，Ⅲ) (Ⅶ，Ⅳ) (Ⅶ，Ⅴ) (Ⅶ，Ⅵ) (Ⅶ，Ⅶ) 说明：组合(Ⅰ，Ⅰ)中，表示树种株数的均匀度等级为Ⅰ，树种蓄积的均匀度等级为Ⅰ，林分株数(或蓄积)的分布均匀度等级见表1。
其他组合依次类推
图 2 树种数为3个时的树种组成多样性指数(ISCD)变化趋势
Figure 2. Trend of diversity index of tree species composition (ISCD) for three species
-
对树种数10个以内的ISCD的变化规律，可以采用“十分法”的分级方法进行均匀度等级划分，即将各树种的株数或蓄积比例的范围划分为10个等份，每变化10%作为一级进行组合。对树种数处于[1，10]的森林，计算其各自不同分布情况下的ISCD值(表3)。
表 3 不同树种组合类型的树种组成多样性指数(ISCD)值
Table 3. Diversity index of tree species composition (ISCD) value of different tree specie composition types
树种数/个 树种组成
形式数/个树种组成
类型数/个ISCD 均值 中位数 最小值 最大值 极差 标准差 1 1 1 1.000 1.000 1.000 1.000 0.000 − 2 5 15 1.880 1.900 1.680 2.000 0.320 0.093 3 8 36 2.883 2.893 2.673 2.993 0.320 0.075 4 8 36 3.895 3.905 3.730 3.970 0.240 0.058 5 7 28 4.926 4.935 4.800 5.000 0.200 0.048 6 5 15 5.935 5.938 5.867 5.987 0.120 0.031 7 3 6 6.956 6.958 6.923 6.983 0.060 0.022 8 2 3 7.975 7.975 7.965 7.985 0.020 0.010 9 1 1 8.991 8.991 8.991 8.991 0.000 − 10 1 1 10.000 10.000 10.000 10.000 0.000 − 总计 41 142 说明：−表示标准差缺失，仅有1个数值无法进行标准差计算 当森林具有a、b 2个树种时，“十分法”下2个树种株数(或蓄积)的比例可以分为9∶1、8∶2、7∶3、6∶4、5∶5这5种中任意一种，即树种组成形式[6]数为5。此外，每种类型还需考虑蓄积(或株数)比例，则又各自有5种可能性，故理论上所有可能的树种混交组合形式应为25种。但由于ISCD赋予树种株数均匀度、蓄积均匀度相同的权重关系，且在考量株数、蓄积均匀度时都是基于树种占比与1/s较差取平方的计算方式，故a树种株数占比为x、蓄积占比为y的森林与株数占比为y、蓄积占比为x的森林拥有相同的ISCD指数值，可认为两者属于同一均匀度分布水平，可进行合并。故25个类型又最终归并为15个，即树种组成类型数为15。
由图3可见：142个树种混交组合中，ISCD随树种数增加呈线性增长趋势，且不同树种数之间ISCD互不重叠。
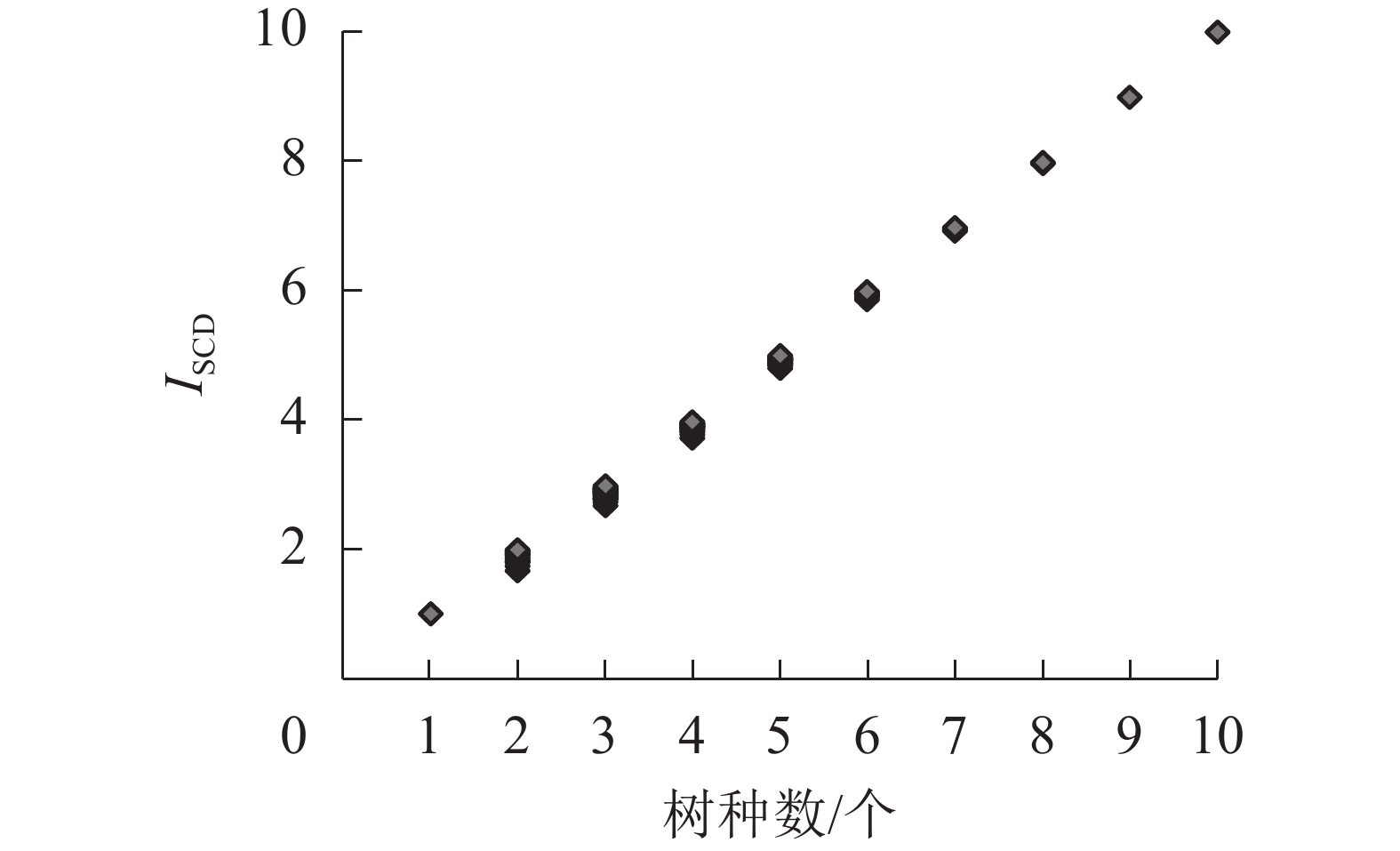
图 3 树种组成多样性指数(ISCD)与树种数的关系
Figure 3. Relationship between diversity index of tree species composition (ISCD) and the number of tree species
综上所述，ISCD随树种数增加呈明显增大趋势。当树种数不变时，ISCD能随树种株数及蓄积(生物量)比例和分布的均匀度、混交度变化而有相应的同向变化。同理，对树种数10个以上的ISCD值，经推论也有相同的规律和特性。
-
以浙江省2009年森林资源连续清查数据中322个针阔混交林样地为材料，计算分析ISCD模型的实际应用情况，并比较ISCD与其他多样性指数在反映林分树种组成中树种丰富度、均匀度及多样性等方面的实用表现。
-
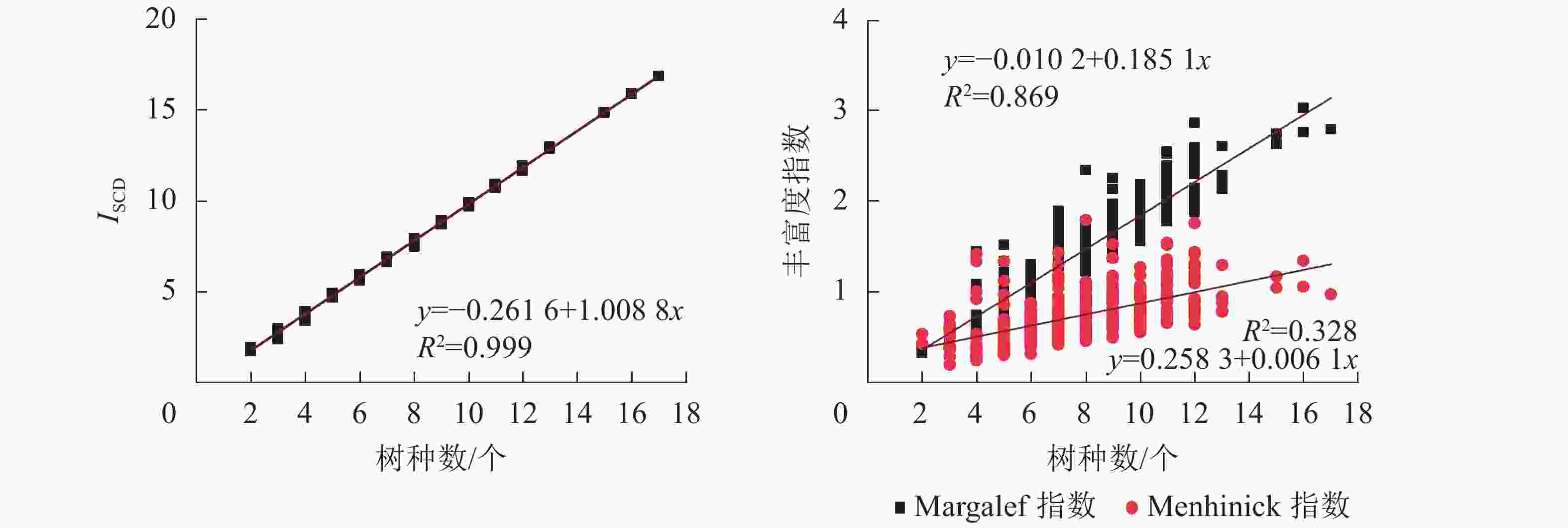
选取Margalef指数[11]、Menhinick指数[11]与ISCD对样地林分丰富度进行计算和对比分析。从图4可见：ISCD随树种数的增多呈上升趋势，具有明显的“分段”现象，表明ISCD对树种数的分异性能强；Margalef指数与Menhinick指数值聚集在较小范围内，随树种数增多呈上升趋势，但变化幅度不大。
图 4 样地树种丰富度分布
Figure 4. Species richness of sample plots
根据不同树种数时各指数的分布形态(图5)，对其进行指数函数、线性函数、对数函数、多项式函数以及幂函数等多种函数拟合，并选择最优拟合模型。结果显示：ISCD、Margalef指数以及Menhinick指数与树种数均呈正相关。ISCD的线性拟合决定系数(R2)达0.999，斜率接近于1，与树种丰富度相关性十分紧密，可信度高。Margalef指数的线性拟合R2为0.869，斜率为0.185 1，与树种丰富度相关性较为紧密，可信度较高。Menhinick指数与树种数的拟合模型R2均未超过0.4，线性斜率为0.006 1，与树种丰富度相关性不明显。表明ISCD比Margalef指数和Menhinick指数对树种丰富度变化的反映更敏感，更具有一致性。
图 5 各丰富度指数与树种数的关系
Figure 5. Relationship between each diversity indices and the number of tree species
-
基于ISCD指数的构造特性，其值中的小数部分(ISCD-U)仅反映树种分布的均匀度，故可单独提取用于比较分析，以消除树种丰富度的影响。ISCD-U指标计算公式为：
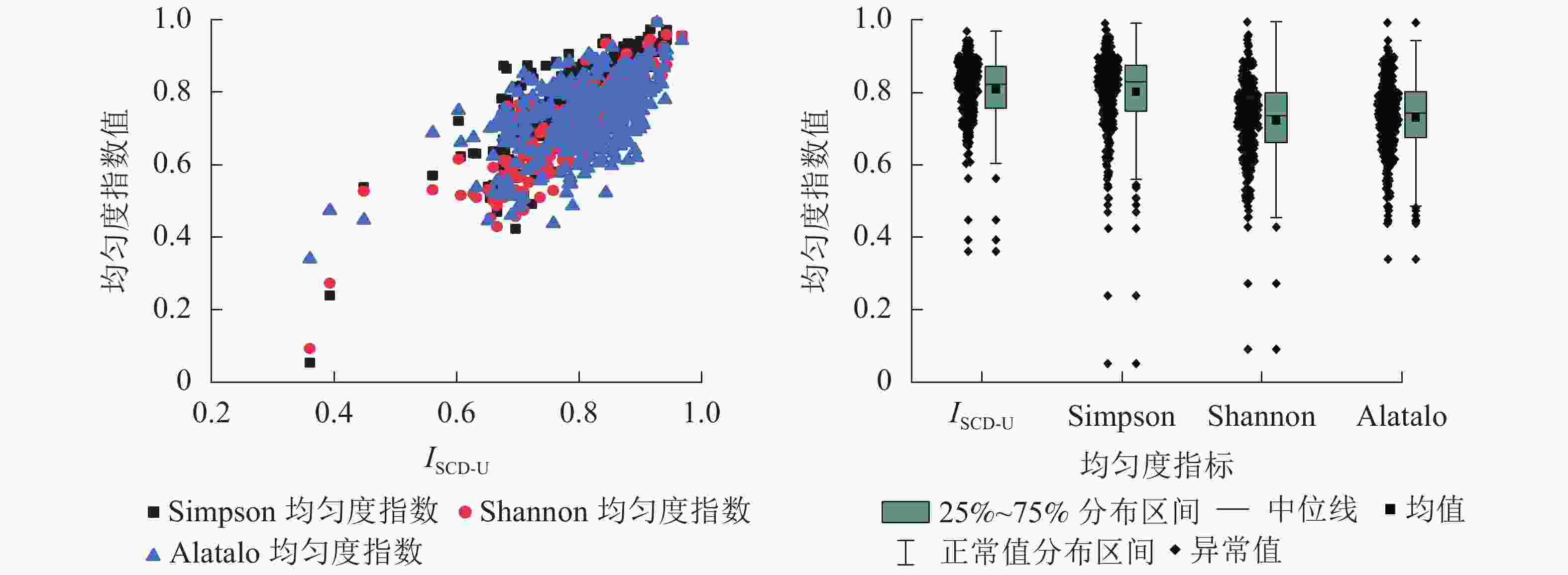
$$ {I_{{\text{SCD-U}}}} = {{I}_{{{\text{SCD}}}}}-s + {\text{1}} = {\text{1}} - \frac{1}{2}\sum\limits_{i = 1}^s {\left[ {{{\left( {\frac{{{v_i}}}{v} - \frac{1}{s}} \right)}^2} + {{\left( {\frac{{{n_i}}}{n} - \frac{1}{s}} \right)}^2}} \right]} 。 $$ (2) 选取α多样性指数中的Shannon均匀度指数[12]、Simpson均匀度指数[12]、Alatalo均匀度指数[13]等与ISCD-U进行均匀度计算和对比分析。各均匀度指数统计结果见表4，依ISCD-U进行升序排列结果见图6。
表 4 针阔混交林样地均匀度指数值
Table 4. Uniformity index values of coniferous and broad-leaved mixed forest
变量名 ISCD-U Simpson均匀
度指数Shannon均匀
度指数Alatalo均匀
度指数均值 0.808 0.801 0.722 0.730 中位数 0.824 0.829 0.737 0.742 方差 0.007 0.013 0.012 0.010 标准差 0.086 0.112 0.111 0.102 标准误 0.005 0.006 0.006 0.006 最小值 0.361 0.052 0.091 0.339 最大值 0.968 0.992 0.994 0.992 极差 0.607 0.940 0.903 0.652 
图 6 样地树种均匀度分布
Figure 6. Evenness of tree species in the sample plot
由表4和图6可知：ISCD-U与Simpson均匀度指数、Shannon均匀度指数以及Alatalo均匀度指数具有较强一致性，且ISCD-U与Simpson均匀度指数分布较为接近，两者均值分别为0.808、0.801，中位数分别为0.824、0.829，最大值和最小值有所差异，且ISCD-U的变动幅度小于Simpson均匀度指数。此外，ISCD-U、Simpson均匀度指数的均值、中位数明显大于Shannon均匀度指数、Alatalo均匀度指数。从分布范围来看，ISCD-U的分布最为集中，对树种均匀程度的评价最为严密。
对ISCD-U、Shannon均匀度指数、Simpson均匀度指数及Alatalo均匀度指数进行Pearson相关分析(表5)表明：ISCD-U与Simpson均匀度指数相关系数为0.840，与Shannon均匀度指数相关系数为0.825，与Alatalo均匀度指数相关系数为0.555。4个指数两两之间相关性均达到极显著水平(P＜0.01)。Simpson均匀度指数与Shannon均匀度指数相关性最高，其次是ISCD-U与Simpson均匀度指数、ISCD-U与Shannon均匀度指数。相关性最低的为ISCD-U与Alatalo均匀度指数。ISCD-U与Shannon均匀度指数、Simpson均匀度指数在反映林分树种组成均匀度方面具有比较一致的灵敏性和分异性。
表 5 均匀度指数之间的相关系数
Table 5. Correlation coefficient between uniformity indexes
均匀度指标 ISCD-U Simpson
均匀度指数Shannon
均匀度指数Alatalo
均匀度指数ISCD-U 1 Simpson
均匀度指数0.840** 1 Shannon
均匀度指数0.825** 0.934** 1 Alatalo
均匀度指数0.555** 0.668** 0.622** 1 说明：**表示在0.01水平上相关极显著(双尾) -
选取具有代表性的Simpson多样性指数[12]、修正Simpson多样性指数[14]、Shannon多样性指数[12]、Shannon多样性幂指数[14]、Hill多样性指数[15]、Mclntosh指数[16]等与ISCD进行多样性的对比分析。
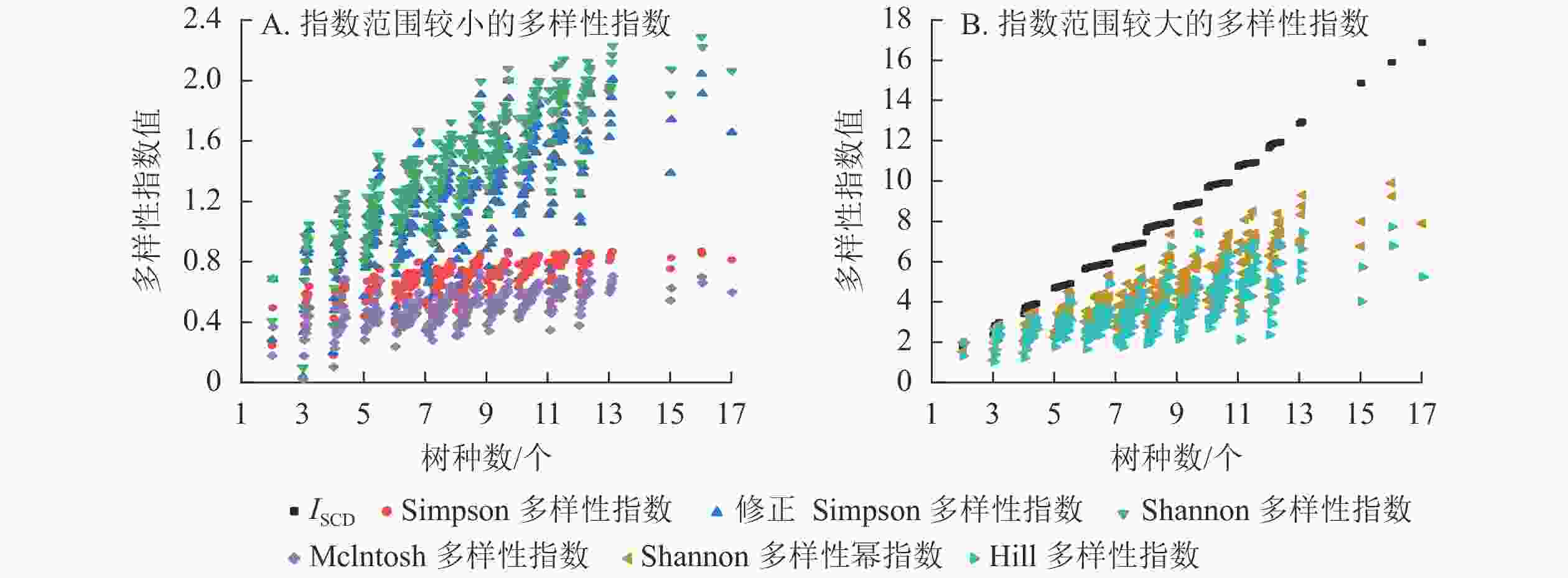
由表6和图7可知：多样性指数按指数范围从大到小依次为ISCD、Shannon多样性幂指数、Hill多样性指数、Shannon多样性指数、修正Simpson多样性指数、Simpson多样性指数、Mclntosh多样性指数，7个指数的均值、中位数、最大值、最小值等都有明显差异。分布形态上，ISCD呈分段聚集，与其他6个指数的分布形态明显不同。Shannon多样性幂指数与Hill多样性指数分布较为接近，Shannon多样性指数与修正Simpson多样性指数分布较为接近，Simpson多样性指数与Mclntosh多样性指数分布较为接近。
表 6 针阔混交林样地的多样性指数值
Table 6. Diversity index values of coniferous and broad-leaved mixed forest
变量名 ISCD Simpson多样
性指数修正Simpson
多样性指数Shannon多样
性指数Mclntosh多样
性指数Shannon多样性
幂指数Hill多样
性指数均值 7.774 0.688 1.228 1.456 0.499 4.576 3.635 中位数 7.776 0.712 1.243 1.468 0.509 4.341 3.467 方差 7.497 0.014 0.128 0.134 0.012 2.662 1.704 标准差 2.738 0.117 0.357 0.366 0.110 1.631 1.305 标准误 0.153 0.007 0.020 0.020 0.006 0.091 0.073 最小值 1.724 0.035 0.035 0.100 0.019 1.106 1.036 最大值 16.860 0.870 2.044 2.291 0.727 9.889 7.719 极差 15.136 0.836 2.009 2.191 0.708 8.783 6.684 
图 7 样地树种多样性分布
Figure 7. Species diversity of the sample plots
由表7可知：7个指数间相关性都达到极显著水平(P＜0.01)。ISCD与其他多样性指数具有极显著的相关性(P＜0.01)，与Shannon多样性幂指数的相关系数最大，为0.840，其次是Shannon多样性指数、修正Simpson指数、Hill多样性指数、Simpson多样性指数以及Mclntosh多样性指数。α多样性指数中，各指数之间普遍具有显著相关性(P＜0.01)，对多样性的评价具有一致性。
表 7 多样性指数之间的相关系数
Table 7. Correlation coefficient between diversity indexes
多样性指标 ISCD Simpson多样
性指数修正Simpson
多样性指数Shannon多样
性指数Mclntosh多样
性指数Shannon多样性
幂指数Hill多样
性指数ISCD 1 Simpson多样性指数 0.684** 1 修正Simpson多样性指数 0.724** 0.967** 1 Shannon多样性指数 0.839** 0.943** 0.965** 1 Mclntosh多样性指数 0.635** 0.967** 0.965** 0.929** 1 Shannon多样性幂指数 0.840** 0.878** 0.952** 0.974** 0.891** 1 Hill多样性指数 0.719** 0.891** 0.975** 0.934** 0.914** 0.967** 1 说明：**表示在0.01水平上相关极显著(双尾) 由图7可知：同一树种数时，ISCD、Simpson多样性指数、修正Simpson多样性指数、Shannon多样性指数、Shannon多样性幂指数、Mclntosh多样性指数以及Hill多样性指数均对样地林分多样性水平具有较为一致的评价；由于对稀有种的不同看法，一旦树种数增加，就会产生2种截然不同的变化：ISCD重视树种数的重要性，强调树种的“存在价值”，认为树种数多，多样性便高，指数就呈不断上升趋势，稀有树种与富集树种的差异更多反映在小数部分。而其余指数则倾向于对树种多度分布均匀的样地赋予更大的指数值。稀有树种的出现并不一定直接提高林分多样性。
在多样性指数中，普遍存在1个指数值对应多种树种数的现象，即存在指标难以区分低丰富度高均匀度群落与高丰富度低均匀度群落的问题，指数的大小并不能有效反映具体的多样性信息，只在相对比较中具有意义。ISCD在反映树种组成多样性上弥补了现有多样性指数的缺陷，更有利于实现对林分树种组成的定量化表征。
-
在对树种组成的定量化描述上，不论是Margalef指数、Menhinick指数，还是Shannon指数、Simpson指数，亦或是Hill指数，都各有其优势与不足。Margalef指数和Menhinick指数等试图权衡丰富度与总丰度的关系，却缺少考虑物种内个体的同质性(均匀性)；在测度树种的丰富度时，以树种数和林分总株数的关系为基础，虽然肯定了稀疏树种与富集树种对群落林分中树种多度的贡献，但对于描述林分树种组成而言仍显不足，其数值具有较大不确定性，即只能判断相对抽象的树种丰富性程度，却无法给出具体丰富度信息等(如林分树种数)。
基于丰度的多样性指数(如Shannon指数和Simpson指数)在物种丰富度的基础上增加了个体数量的信息，考虑了异质性，却依旧无法代表一个群落的真正“多样性”。对于均匀性的度量方案似乎是无穷无尽的，有许多方法可以根据“均匀性”的不同定义来估计，这使得对均匀性的概念并不十分清晰[17]。目前常用的Simpson均匀度指数与Shannon均匀度指数将均匀度定义为群落的实测多样性与理论最大多样性的比率。
Shannon指数和Simpson指数及变体往往被认为可以将物种丰富度和均匀度巧妙地整合成全方位的衡量标准而广泛使用。然而，这些复合指数对多样性的度量依旧有限：①Shannon指数植根于信息理论，是一种熵，量化的是随机挑选得到的某个个体物种身份的不确定性强弱(不确定性强，多样性高)。Simpson指数也是广义的熵[18]，量化的是从数据集中随机挑选的2个个体不代表同一物种的概率。指数作为熵，反映的是物种集合体与多样性有关的不同特性，衡量的是不确定性，并不是真正的多样性[19]。虽然熵的变化在数学上与物种丰富度相关，但在很大程度上它们与丰富度的关系已被证明是不一致的[20-21]。此外，熵及其变化因其可能掩盖多样性各组成部分之间的差异而显得不足，致使有学者认为复合指数在很大程度上是没有意义[22]。②物种丰富度和均匀度之间可能存在反向关系，在复合指数中会相互抵消，并不能得到与直观感觉一致的结果[23]。③复合指数对多样性和均匀性的权重高于丰富性，且对稀有物种与丰富物种赋予不同的权重，这掩盖了物种丰富度的重要性。
HILL[24]提出希尔数(hill numbers)，即有效物种数，用以量化多样性。有效物种数借助参数实现对丰富物种与稀有物种的权重控制，并能服从生物学家多样性概念中隐含的复制原则或加倍性质，被认为是物种多样性丰度的最佳选择[25]。然而同样有学者提出，有效物种数的使用存在一定局限性[17]。
ISCD以树种数量直接作为多样性丰富度，指数值接近实际树种数显得更加简洁、直观、有效，可根据指数值快速反推单个样地树种数。这是其他α多样性指数无法实现的。
ISCD对均匀度的评价方法以林分中树种的个数及各树种的属性比例作为变量，从树种的株数分布和蓄积分布2个方面衡量森林中树种分配的均匀性。通过各树种株数以及蓄积比例的不同，对两者的作用有了明确区分。此外，ISCD-U指标以现有林分与同一树种数下的理想林分(树种完全均匀分布)之间存在的差距进行均匀性评价，是一种新视角下的均匀性度量方式。
从指数构造角度而言，ISCD也具有科学性。物种丰富度和均匀度之间存在一定关系[26]。许多学者倾向于认为物种丰富度与均匀度应该是相对独立的[20, 27]，但实际发现均匀度总是不可避免地受到丰富度的制约，两者依旧存在相关关系。ISCD将指数丰富度信息与均匀度信息进行了明确分离，使其各自独立而不再相互作用。
-
从指数表现来看，ISCD对林分树种丰富度反映灵敏，有着很好的区分性，弥补了现有指数对林分树种数反映表征模糊、指数范围重叠、区分不灵敏等不足。在反映树种组成多样性综合效应时，比其他指数有更好的区分性，同时与其他指数存在显著相关性，表明ISCD具有与其他多样性指数相同的理论基础，其本质相同但形式与侧重点不同。
对于α多样性指数而言，当用直径、树高或其他结构分类变量来代替物种时，它就可以反映林分结构多样性，体现对应林分组成结构属性特征[9]，例如Simpson大小多样性指数、Shannon大小多样性指数、Simpson大小分化度指数、Shannon大小分化度指数等林木大小多样性指数[28]以及树高多样性指数等。同理，ISCD在后续应用时，亦可衍生类似指数，例如以胸高断面积、生物量、生产力替代蓄积使用，ISCD指数同样具有一定的可拓展性。但对于描述复杂树种结构而言，依旧存在不足。如何体现树种结构的空间分布，如何对不同树种属性进行合理的权重设置，仍是ISCD未来需要攻克的难点。
-
ISCD在数量化表达林分树种组成多样性时，有效地将树种丰富度与树种株数、蓄积均匀性既分离又融合在一起，是一个较全面反映树种组成多样性信息的综合指标。它对林分树种组成的丰富度反映比其他多样性指数更加灵敏，分异性更强，对林分树种组成的均匀度有着与其他多样性指数一致的灵敏度和区分度，其数值大小还体现出现有林分与理想林分的差距，这也为评价林分树种组成均匀程度提供了一种新思路。相互独立的丰富度、均匀性信息使得指数值本身具有意义，解决了对低丰富度高均匀度、高丰富度低均匀度等不同林分树种组成类型难以有效区分这一难题，有利于准确描述树种组成多样性。
Construction of diversity index of tree species composition
-
摘要:
目的 构建数量化指标以定量表达林分树种组成特征，是精准经营管理森林的技术基础。 方法 应用生物多样性理论，根据树种组成的特性和经营管理要求，构建了林分树种组成多样性指数(ISCD)。采用“十分法”，分析了不同树种数下指数的变化规律及基本特性。以国家森林资源连续清查中浙江省322个针阔混交林样地为应用对象，对ISCD与现有的α多样性指数进行了对比分析。 结果 ISCD涵盖了林分中树种数、树种相对多度和树种蓄积比例等信息，突出体现树种数的同时，充分表达了树种组成的均匀性与混交程度。ISCD可完整、独立和有效地表达树种组成的变化特性。与α多样性指数相比，ISCD提高了对树种数判别的分异性和灵敏性，可严密地评价树种结构的均匀度和混交度，合理有效地反映树种多样性。 结论 与α多样性指数相比，构建数量化指标能更细致、全面、有针对性地定量化表征林分树种组成多样性，解决了低丰富度高均匀度、高丰富度低均匀度等不同林分树种组成类型难于有效区分的难题。图7表7参28 -
关键词:
- 林分 /
- 树种组成多样性指数(ISCD) /
- 多样性指数 /
- 树种数 /
- 均匀度
Abstract:Objective This study aims to construct quantitative indicators to quantitatively express the composition characteristics of tree species, which is the technical basis for accurate forest management. Method Based on the theory of biodiversity and the characteristics of tree species composition and management requirements, the diversity index of tree species composition (ISCD) was constructed. The variation pattern and basic characteristics of index under different tree species were analyzed by “ten method”. 322 coniferous and broad-leaved mixed forest plots in the inventory of national forest resources of Zhejiang Province were selected as the application objects. ISCD and existing major α-diversity indices were compared. Result ISCD covered information on the number of tree species, the relative abundance of tree species and the proportion of tree species in the stand, which not only highlighted the number of tree species, but also fully expressed the uniformity and mixing degree of tree species composition. ISCD could express the changing characteristics of tree species composition completely, independently and effectively. Compared with the major α-diversity indices, ISCD improved the differentiation and sensitivity of tree species, closely evaluated the uniformity and mixing degree of tree species structure, and reasonably and effectively reflected the tree species diversity. Conclusion Compared with the majorα-diversity indices, the construction of quantitative index can quantitatively characterize the diversity of tree species composition in a more detailed, comprehensive and targeted manner, and solve the problem that it is difficult to effectively distinguish the composition types of tree species in different stands, such as low richness and high uniformity, high richness and low uniformity. [Ch, 7 fig. 7 tab. 28 ref.] -
植物种群的空间分布格局是指种群在水平空间上的配置和分布状况[1]，除了种群自身特性和环境条件因素与其形成密切相关外[2]，种间关系也是促使其形成的主要动力之一[3]，在判断植物种间关系时，生态学家们通常会运用种间联结性分析来探究物种之间的内在联系[4]。此外，生态位的重叠程度在一定程度上能够反映物种联结关系以及空间配置关系[5-6]。对植物种间关系及空间分布格局的研究，有助于认识种群与生境的相互关系、空间资源获取能力与生态适应对策，预测群落消长动态，是深入了解维持树木物种共存机制，并了解产生空间格局的过程的重要手段[7-9]，对于正确认识群落的组成、功能及演替规律具有重要意义。次生林是中国森林资源的主体，它既保持着原始森林的物种组成成分与生境，又与原始森林在结构组成、林木生长、生产力、林分环境和生态功能等诸多方面有着显著的不同，原始林退化导致的次生林面积扩大将引起森林生态系统中生物多样性的下降[10]。如何恢复和保护次生林群落的物种多样性成为生态学家面临的重要问题。而对森林木本植物的空间分布格局及种间关系的研究有助于揭示群落结构的形成机制与潜在的生态学过程，对次生林的经营抚育具有一定指导意义[11]。以松林、松阔混交林和常绿阔叶林中幼龄林为主体的天然次生林是浙江省建德市的森林资源主体，主要由被过度干扰破坏的天然林地逐渐恢复、演替而来[12]。次生林中仍保有原始森林的部分物种，但不同类型次生林在群落结构、林木年龄组成、植物生产力及生境等方面都存在显著差异[13]。本研究对浙江建德的次生林群落进行每木调查，分析主要树种间的相互关系及空间分布格局特征，以增强对该区域次生林群落结构特征和空间分布格局的认识，促进区域生物多样性保护与木本植物资源的可持续利用，预测群落的演替方向并探索其驱动力来源，进而为该区域次生林群落的恢复、改造及抚育经营提供依据，更好发挥其生态社会效益。
1. 研究区概况
研究区位于浙江省建德市新安江林场(29°29′N，119°16′E)，属亚热带北缘季风气候，温暖湿润，四季分明，年平均气温为16.9 ℃，最冷月平均气温为4.7 ℃，最热月平均气温为29.2 ℃，年均降水量为1 504.0 mm。据《中国植被》区划，该地区森林植被属亚热带常绿阔叶林北部亚地带，地带性植被为常绿阔叶林。主要森林植被类型有常绿阔叶林、落叶阔叶林、常绿落叶阔叶混交林、针阔混交林等[14]。
2. 研究方法
2.1 样地设置及调查
在实地踏查的基础上，在浙江建德典型常绿阔叶林、松阔混交林和松林群落中分别设置面积为100 m×100 m的样地(表1)，用木桩、塑料带进行围封标记。将每块样地划分为25小块(20 m×20 m)，并以此为基本单位对乔木层进行每木调查。记录样地群落类型、海拔、坡度、坡向、土壤等环境因子；记录样方中胸径≥5 cm的木本植物的基础数据，包括种名、树高、胸径、冠幅及其相对应的坐标[15-16]。
表 1 样地基本信息Table 1 Basic information of sample plots样地类型 海拔/m 纬度(N) 经度(E) 坡度/(°) 坡向 土壤类型 地点 常绿阔叶林 172 29°40′ 119°23′ 44 西 红壤 杨村桥镇徐坑村 松阔混交林 165 29°28′ 119°12′ 38 南 红壤 新安江林场朱家埠林区 松林 90 29°21′ 119°09′ 33 东 红壤 新安江林场朱家埠林区 2.2 重要值
重要值(IV)计算[17]：IV=(相对多度+相对显著度+相对频度)/3×100%。
2.3 生态位重叠
采用Pianka重叠指数计算物种间的生态位重叠系数，公式[18]如下：
$${O_{ik}}{\rm{ = }}\mathop \sum \limits_{j = 1}^w \left( {{P_{i\!j}}{P_{k\!j}}} \right) \div \sqrt {{{\left( {\mathop \sum \limits_{j = 1}^w {P_{i\!j}}} \right)}^2}{{\left( {\mathop \sum \limits_{j = 1}^w {P_{k\!j}}} \right)}^2}} \text{。}$$ 其中：Oik为种i和种k的生态位重叠系数[1]；w为划分的资源位总数；Pij和Pkj分别是种i和种k在资源位j中的重要值占该物种在整个资源中总重要值的比例。Oik的值域为[0，1]，当2个种对群落中所有的资源都不存在共享状态时，该种对之间生态位完全不重叠，其值为0；当2个种对群落中所有资源利用完全重叠时，该种对的生态位重叠程度为1，达到最大状态。
2.4 空间分布格局
2.4.1 种内空间分布格局
Ripley’s K(r)函数是进行种内空间分布格局分析的基础函数，公式如下[19]：
$$ K\left( r \right) = \frac{A}{{{n^2}}}\sum\limits_{p = 1}^n {\sum\limits_q^n {e_{pq}^{ - 1}} } {I_r}{\rm{(}}{u_{pq}}{\rm{)}}\text{。} $$ 其中：r为分析的空间尺度(m)，A为样方面积(m2)，n为植物种个体数，upq表示点p和点q之间的距离(m)；Ir(upq)为指示函数，当upq≤r时，Ir(upq)=1，当upq＞r时，Ir(upq)=0；epq为权重值，用于边缘校正。为了更直观地解释实际的空间格局，通常用Ripley’s L(r)函数表示：
$$L\left( r \right) = \sqrt {\frac{{K\left( r \right)}}{\text{π} }} {\rm{ - }}r\text{。}$$ 当L(r)=0，种群分布类型为随机分布，对种群的聚集分布研究基于随机分布的基础，以样地中的任意一点为圆心，r为半径画圆，如果在圆中出现的个体数多于随机状态下的个体数，那么表示该种群呈现聚集分布；当圆中出现的个体数少于随机分布状态下的个体数时，该种群呈现均匀分布[20-22]。采用Monte-Carlo模拟99%置信区间，进行结果偏离随机状态的显著性检验。若L(r)值位于置信区间之上，种群呈聚集分布，L(r)值位于置信区间之下，种群呈均匀分布，L(r)值位于置信区间之内，种群呈随机分布[23]。
2.4.2 种间空间分布格局
种间空间分布格局基础函数计算公式[24]如下：
$${K_{12}}\left( r \right) = \frac{A}{{{n_1}{n_2}}}\sum\limits_{g = 1}^n {\sum\limits_f^n {w_{gf}^{ - 1}} } {I_r}({u_{gf}})\text{。}$$ 其中：n1和n2分别为种1和种2的个体数，f和g分别代表种1和种2的个体。同样，用L12(r)取代K12(r)，公式为：
$${L_{12}}\left( r \right) = \sqrt {\frac{{{K_{12}}\left( r \right)}}{\text{π} }} {\rm{ - }}r\text{。}$$ 当L12(r)=0，表明2个种在r尺度下无关联；当L12(r)＞0，表明两者为空间正关联；当L12(r)＜0，表明两者为空间负相关。采用Monte-Carlo模拟99%置信区间，进行结果偏离随机状态的显著性检验。当L12(r)值位于置信区间之上，2个变量显著正相关；L12(r)值位于置信区间之下，2个变量显著负相关；L12(r)值位于置信区间之内，2个变量相互独立[23]。本研究根据实际样地面积，在参考同类研究及毗邻地区森林群落空间格局研究的基础上[25-26]，将格局分析的尺度限定为0~25.0 m。
2.5 种间联结
2.5.1 总体联结性检验
采用方差比率法来测定各类型次生林群落中主要树种间的总体联结性，并利用统计量W来检验总体联结是否显著，计算公式[27]如下：
$${V_{\rm{R}}} = \frac{{\dfrac{1}{N}\displaystyle\sum\limits_{z = 1}^N {{{({T_z} - t)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^S {(1 - {P_i})} }}\text{。}$$ 其中：VR为方差比率，N为样方总数，
$ T_z $ 为样方$ z $ 内出现的目标物种总数；t为样方中物种的平均数，S为总物种数，Pi为物种i的频度。以VR作为不同类型次生林中主要树种总体联结性指数，在独立性零假设条件下，VR期望值为1，即当VR=1时认为种间无联结；若VR＜1则表示物种间存在正联结；若VR＜1则表示物种间存在负联结。对于VR偏离1的显著程度采用统计量W来验证，W=VRN，若$W{\text{＜}}$ ${\textit{χ}}_{0.95}^2\left( N \right)$ 或$W{\text{＞}}{\textit{χ}} _{0.05}^2\left( N \right)$ 则说明种间总体联结性性显著，若${\textit{χ}} _{0.05}^2\left( N \right) {\text{＞}}W {\text{＞}} {\textit{χ}}_{0.95}^2\left( N \right)$ 则说明种间总体联结性不显著[28]。2.5.2 种间联结性分析
采用经Yates连续校正系数纠正的χ2统计量对种间联结性进行定性研究。公式[18]如下：
$${\textit{χ} ^2} = \frac{{N{{[ad - bc - 0.5N]}^2}}}{{(a + b)(b + d)(a + c)(c + d)}}\text{。}$$ 其中，N为取样总数，
$ a $ 为2物种均出现的样方数，b、c分别为2个种单独出现的样方数，d为2物种均不出现的样方数。当$ ad-bc=0 $ 时，2个种相互独立；$ ad-bc{\text{＞}}0 $ 时，2个种之间呈正联结；$ ad- $ bc＜0时，2个种之间呈负联结。${\textit{χ}}^{2}$ ＜3.841时，表示种间联结性不显著；当3.841＜${\textit{χ}}^{2}$ ＜6.635时，表示种间联结性显著；当${\textit{χ}}^{2}$ ＞6.635时，表示种间联结性极显著[17]。为避免出现分母为0无法计算分析的状况，把a、b、c、d凡是为0的都加权为1[29-30]。2.5.3 种间相关性测定
本研究以多度作为Spearman秩相关系数的数量指标，对种对间的线性关系做定量分析，计算公式[31]如下：
$$r\left( {i,k} \right) = 1 - \frac{{6\displaystyle\sum\limits_{z = 1}^N {{{\left( {{x_{iz}} - {{\bar x}_i}} \right)}^2}} {{\left( {{x_{kz}} - {{\bar x}_k}} \right)}^2}}}{{{N^3} - N}}\text{。}$$ 其中，
$ r\left(i,k\right) $ 是种$ i $ 和种$ k $ 在样方$ z $ 中的Spearman秩相关系数；$ N $ 为样方总数；$ {x}_{iz} $ 和$ {x}_{kz} $ 分别是种$ i $ 和种$ k $ 在样方$ z $ 中的秩；$ {\bar{x}}_{i} $ 和$ {\bar{x}}_{k} $ 分别是种$ i $ 和种$ k $ 在所有样方中多度的平均值。$ r\left(i,\;k\right) $ 的值域为[−1, 1]，正值表示正相关，负值表示负相关。3. 结果与分析
3.1 重要值
根据重要值大于5%选出各植被类型主要树种。常绿阔叶林中主要树种是青冈Cyclobalanopsis glauca、石栎Lithocarpus glaber、苦槠Castanopsis sclerophylla及木荷Schima superba等4种；松阔混交林的主要树种分别是马尾松Pinus massoniana、苦槠、杉木Cunninghamia lanceolata、檵木Loropetalum chinense、石栎等5种；松林的主要树种分别是马尾松、杉木、苦槠、化香Platycarya strobilacea、枫香Liquidambar formosana等5种。
3.2 生态位重叠
从表2可以看出：在常绿阔叶林中，主要树种之间生态位重叠程度最高的是木荷-石栎(0.861 4)、其次是苦槠-青冈(0.615 4)，最低的是苦槠-木荷(0.377 2)；在松阔混交林中，重叠程度最高的是檵木-苦槠(0.801 8)，其次是马尾松-石栎(0.753 1)，最低的是石栎-杉木(0.340 9)；在松林中，重叠程度最高的是枫香-化香(0.757 5)，其次是枫香-苦槠(0.720 1)，最低的是苦槠-马尾松(0.442 7)。
表 2 不同森林类型主要树种生态位重叠数值矩阵Table 2 Niche overlap of dominant tree species of different forest types常绿阔叶林 松阔混交林 松林 树种 苦槠 木荷 青冈 树种 檵木 苦槠 马尾松 石栎 树种 枫香 化香树 苦槠 马尾松 木荷 0.377 2 苦槠 0.801 8 化香 0.757 5 青冈 0.615 4 0.518 2 马尾松 0.631 2 0.632 4 苦槠 0.720 1 0.625 8 石栎 0.421 9 0.861 4 0.473 3 石栎 0.451 3 0.458 4 0.753 1 马尾松 0.676 9 0.567 6 0.442 7 杉木 0.393 7 0.521 8 0.646 2 0.340 9 杉木 0.466 2 0.470 7 0.600 1 0.567 5 3.3 空间分布格局
3.3.1 种内空间分布格局
在所有研究样地中，主要树种在0~25.0 m的尺度内均表现为显著的聚集分布(P＜0.05)(图1~3)。
图 1 常绿阔叶林主要树种空间分布格局Figure 1 Spatial distribution pattern of dominant tree species in evergreen broad-leaved forest
图 2 松阔混交林主要树种空间分布格局Figure 2 Spatial distribution pattern of dominant tree species in mason pine and broad-leaved mixed forest
图 3 松林主要树种空间分布格局Figure 3 Spatial distribution pattern of dominant tree species in mason pine forest3.3.2 种间空间分布格局
常绿阔叶林主要树种空间分布格局特征如下(图4)：青冈-石栎在0~25.0 m尺度上均呈现负相关，其中6.0~10.0 m、15.0~17.0 m尺度上负相关达到显著(P＜0.05)；青冈-木荷在0~25.0 m尺度上均为负相关，其中8.0~14.0 m尺度范围内达到显著(P＜0.05)；石栎-木荷在0~25.0 m尺度上均呈现显著的正相关(P＜0.05)。其他种对的空间关联性则以不显著相关为主。
图 4 常绿阔叶林主要树种间空间分布格局图Figure 4 Spatial distribution pattern of dominant tree species in evergreen broad-leaved forest松阔混交林主要树种空间分布格局特征如下(图5)：马尾松-石栎在0~25.0 m尺度上呈现正相关，10.0~25.0 m尺度内达到显著(P＜0.05)；苦槠-石栎在0~20.0 m尺度范围内为正相关，其中7.0~8.0 m尺度上达到显著(P＜0.05)，而在20.0~25.0 m尺度范围内呈现不显著负相关。其他种对的空间关联性以不显著相关或无关联为主。
图 5 松阔混交林主要树种间空间分布格局图Figure 5 Spatial distribution pattern of dominant tree species in mason pine and broad-leaved mixed forest松林主要树种间空间分布格局特征如下(图6)：马尾松-化香在0~25.0 m尺度上为负相关，其中4.0 m时达到显著(P＜0.05)；杉木-苦槠在0~25.0 m尺度范围内为正相关，其中15.0~25.0 m尺度上达到显著(P＜0.05)；杉木-化香在0~25.0 m尺度范围内为负相关，其中7.5~17.0 m尺度上达到显著(P＜0.05)；化香-枫香在0~25.0 m尺度范围内表现为正相关，其中12.0~13.0 m尺度上达到显著(P＜0.05)。除此之外其他种对的空间关联性表现为不显著相关或无关联。
图 6 松林主要树种间空间分布格局图Figure 6 Spatial distribution pattern of dominant tree species in mason pine forest3.4 种间联结
3.4.1 总体联结性
各类型次生林的方差比率(表3)结果表明：3种类型次生林主要树种的总体关联性均为不显著正关联。
表 3 不同森林类型主要树种的总体关联性Table 3 Overall interspecific associations among dominant tree species of different forest types样地类型 方差比率 W ${\; \textit{χ}^{2}_{0.95}(N)} $，${ \; \textit{χ}^{2}_{0.05}(N)} $ 结果 常绿阔叶林 1.389 34.722 14.611, 37.652 不显著正关联 松阔混交林 1.397 34.930 14.611, 37.652 不显著正关联 松林 1.199 29.966 14.611, 37.652 不显著正关联 3.4.2 种间联结性检验
χ2检验结果表明(表4)：样地中所有类型次生林的主要树种种对均呈不显著的正联结(χ2＜3.841，
$ ad-bc $ ＞0)。表 4 不同森林类型的种间联结χ2统计量矩阵Table 4 Value of χ2 of different forest types常绿阔叶林 松阔混交林 松林 树种 苦槠 木荷 青冈 树种 檵木 苦槠 马尾松 杉木 树种 枫香 化香 马尾松 杉木 木荷 0.001 苦槠 1.223 化香 0.179 青冈 0.230 0.092 马尾松 1.103 1.103 马尾松 0.230 1.103 石栎 0.039 0.001 0.230 杉木 0.001 0.001 0.010 杉木 0.020 0.179 0.230 石栎 0.089 0.089 0.069 0.110 苦槠 2.214 0.069 0.038 0.368 3.4.3 种间相关性分析
据图7可知：在常绿阔叶林中，呈负相关的种对有苦槠-木荷、木荷-青冈和青冈-石栎等3对，其中木荷-青冈和青冈-石栎种对的负相关达极显著(P＜0.01)；呈正相关的有苦槠-青冈、苦槠-石栎和木荷-石栎等3对，其中木荷-石栎种对的正相关达到极显著(P＜0.01)。在松阔混交林中，呈现负相关的种对有檵木-杉木、檵木-石栎2对；其余8对均呈正相关，其中马尾松-石栎的正相关达极显著(P＜0.01)。在松林中，呈现负相关的种对有枫香-杉木、化香-马尾松、化香-杉木、化香-苦槠和马尾松-苦槠等5对，其中化香-杉木的负相关达显著(P＜0.05)；其余5对呈正相关，其中枫香-苦槠的正相关达显著(P＜0.05)。
图 7 不同森林类型种间Spearman秩相关半矩阵图Figure 7 Semi-matrix of Spearman’s rank correlation coefficients of dominant tree species of different forest types4. 讨论
森林在向顶级群落演替的过程中，植物种内空间分布格局一般会由聚集分布渐渐过渡为随机分布[12]，而在本研究中，0~25.0 m尺度上不同类型次生林的主要树种均呈显著(P＜0.05)聚集分布，这说明样地群落还未进入演替成熟期。物种自身的生物学特性是造成群落演替过程中物种聚集分布的主要原因，即相同物种对环境等条件有着相似的需求[32]。样地群落种间生态位重叠程度也能佐证其所处的演替阶段，顶级群落中树种间的生态位重叠程度一般处在较低的水平，即树种间的竞争并不活跃，这是因为经过长时间演替后，群落趋于稳定，内部树种间达到了一种相对平衡的状态[33-34]，主要树种间的生态位重叠程度仍普遍较高，群落整体呈正关联，正相关种对仍有较高占比。这反映了群落中的主要树种具有相似的环境需求和生态适应性，由此造成了样地中主要树种的聚集分布。此外，种子的扩散限制和生境异质性也被认为是影响物种分布的主要因素[20]，样地中主要树种的种子传播方式以重力传播为主，种子传播距离有限，多聚集在母树周围，离母树越远种子越少，这也导致了树种的聚集分布。在松林中，马尾松和杉木作为建群早期先锋种最先入侵林地，在光竞争中占据优势，对光的有效利用是形成林分空间格局的主要决定因素[35]，因而马尾松和杉木与群落中其他优势树种多呈负空间关联。枫香幼树稍耐荫，所以与群落中其他优势树种多呈正空间关联。在松阔混交林中，主要树种间空间关联显著程度较低，这或许与群落中的针叶树种同群落中其他较晚发育起来的常绿阔叶树种产生了垂直分层现象有关，这种垂直分层现象能够减轻群落内的光竞争，进而影响群落内的树种空间分布格局。马尾松和杉木作为早期先锋树种入侵林地后，逐渐改善了立地条件，为其他树种进入群落创造了条件，使得松林能够向松阔混交林方向演替。随后由于马尾松和杉木生物学特性在垂直结构上与其他树种产生了分层现象，加之密度制约和扩散限制等因素[12]共同作用，群落中的常绿阔叶树种逐渐获得更多的环境资源并对针叶树种和落叶阔叶树种的幼苗更新产生负作用，松阔混交林逐渐向常绿阔叶林演替。这种演替机制与XIANG等[9]的研究结果一致，即在不发生干扰的情况下，次生林群落中的不耐荫落叶树种将逐渐被耐荫的常绿阔叶树种所取代。
通过比较不同森林类型主要树种组成可以发现：3类森林群落的主要树种组成存在差异，落叶阔叶树种枫香和化香仅出现在松林主要树种中，而松阔混交林中已经没有落叶树种，但出现了常绿阔叶树种石栎和檵木。在常绿阔叶林中，主要树种则由木荷及青冈、石栎和苦槠等3种壳斗科Fagaceae树种组成。树种组成的变化是群落演替的结果，森林经营管理可根据此对松林和松阔混交林进行适当抚育，伐除部分针叶树种及清理林内枯立木，改善林分内的光照条件，促进常绿阔叶树种的生长。在常绿阔叶林中，则可通过修枝来改善林内光照条件，也可通过为森林土壤施加养分来改善目标树种的营养状况，通过人为栽种苗木等手段来加快木荷、石栎等目标树种的更新、生长和郁闭，促进森林群落向顶级群落发展并促进生物多样性的恢复。
本研究通过方差比率法、χ2检验和Spearman秩相关系数检验，对不同类型次生林群落种间的联结性和相关性进行了分析。其中，χ2检验结果是由种对的二元数据转换计算而来，反映的是物种能否共存和共存的概率，不能表达低显著度种对的内在相关性情况和强度。Spearman秩相关系数属定量检验方法，能够在一定程度上检验种对数量关系上的变化，对种对间的相关性及其显著性水平更为敏感。Spearman秩相关系数属定量检验与定性的方差比率法、χ2检验结合使用能够更全面地反映物种的种间关系[36]。
5. 结论
通过测度常绿阔叶林、松阔混交林和松林群落中主要树种的生态位重叠程度、空间分布格局和种间联结分析可以发现：本研究各群落乔木层主要树种在空间分布格局中独立性相对较强，物种间虽存在比较相似的环境资源需求，但种间联结关系比较松散，群落演替尚未进入成熟期。此外也可以看出：树种间的空间分布格局、联结性与种群的生态位重叠之间存在密切关联。一般情况下，群落内优势树种种间正联结性越强，其生态位重叠程度越高，种间负联结性越强，生态位重叠程度越低[37]。样地群落的总体关联性检验结果显示：各群落种间总体关联性呈不显著的正相关。χ2检验发现：多数种对都呈不显著的正联结，这与各群落物种生态位重叠程度的分析结果基本吻合。各群落主要树种间的Spearman秩相关分析结果与种间空间关联性结果也有比较一致的表现，这也说明植物种间关系对植物种群空间分布格局的形成有重要意义。本研究可为进一步揭示物种自身生物特性、环境条件及种间关系等综合作用下的种群空间分布格局形成机制提供依据，但群落中植物种间关系及空间分布格局是处在动态变化过程中的，本研究结果仅反映某一特定时间节点的群落状态，有待长期的群落动态监测研究。
-
图 1 树种数为2个时的树种组成多样性指数(ISCD)变化趋势
Figure 1 Trend of diversity index of tree species composition (ISCD) for two species
图 2 树种数为3个时的树种组成多样性指数(ISCD)变化趋势
Figure 2 Trend of diversity index of tree species composition (ISCD) for three species
图 3 树种组成多样性指数(ISCD)与树种数的关系
Figure 3 Relationship between diversity index of tree species composition (ISCD) and the number of tree species
图 5 各丰富度指数与树种数的关系
Figure 5 Relationship between each diversity indices and the number of tree species
表 1 树种数为3个时的株数(或蓄积)分布均匀度等级
Table 1. Distribution uniformity grade of plants number (or volume) of 3 tree species
分布均匀
度等级树种a
占比树种b
占比树种c
占比Simpson均匀
度指数Ⅰ 1/9 1/9 7/9 0.622 Ⅱ 1/9 2/9 6/9 0.773 Ⅲ 1/9 3/9 5/9 0.853 Ⅳ 1/9 4/9 4/9 0.879 Ⅴ 2/9 2/9 5/9 0.906 Ⅵ 2/9 3/9 4/9 0.966 Ⅶ 3/9 3/9 3/9 1.000 
下载: 导出CSV
表 2 树种均匀性分布类型
Table 2. Summary of tree species uniformity distribution types
树种株数分布
均匀度等级树种蓄积分布均匀度等级 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅰ (Ⅰ，Ⅰ) (Ⅰ，Ⅱ) (Ⅰ，Ⅲ) (Ⅰ，Ⅳ) (Ⅰ，Ⅴ) (Ⅰ，Ⅵ) (Ⅰ，Ⅶ) Ⅱ (Ⅱ，Ⅰ) (Ⅱ，Ⅱ) (Ⅱ，Ⅲ) (Ⅱ，Ⅳ) (Ⅱ，Ⅴ) (Ⅱ，Ⅵ) (Ⅱ，Ⅶ) Ⅲ (Ⅲ，Ⅰ) (Ⅲ，Ⅱ) (Ⅲ，Ⅲ) (Ⅲ，Ⅳ) (Ⅲ，Ⅴ) (Ⅲ，Ⅵ) (Ⅲ，Ⅶ) Ⅳ (Ⅳ，Ⅰ) (Ⅳ，Ⅱ) (Ⅳ，Ⅲ) (Ⅳ，Ⅳ) (Ⅳ，Ⅴ) (Ⅳ，Ⅵ) (Ⅳ，Ⅶ) Ⅴ (Ⅴ，Ⅰ) (Ⅴ，Ⅱ) (Ⅴ，Ⅲ) (Ⅴ，Ⅳ) (Ⅴ，Ⅴ) (Ⅴ，Ⅵ) (Ⅴ，Ⅶ) Ⅵ (Ⅵ，Ⅰ) (Ⅵ，Ⅱ) (Ⅵ，Ⅲ) (Ⅵ，Ⅳ) (Ⅵ，Ⅴ) (Ⅵ，Ⅵ) (Ⅵ，Ⅶ) Ⅶ (Ⅶ，Ⅰ) (Ⅶ，Ⅱ) (Ⅶ，Ⅲ) (Ⅶ，Ⅳ) (Ⅶ，Ⅴ) (Ⅶ，Ⅵ) (Ⅶ，Ⅶ) 说明：组合(Ⅰ，Ⅰ)中，表示树种株数的均匀度等级为Ⅰ，树种蓄积的均匀度等级为Ⅰ，林分株数(或蓄积)的分布均匀度等级见表1。
其他组合依次类推
下载: 导出CSV
表 3 不同树种组合类型的树种组成多样性指数(ISCD)值
Table 3. Diversity index of tree species composition (ISCD) value of different tree specie composition types
树种数/个 树种组成
形式数/个树种组成
类型数/个ISCD 均值 中位数 最小值 最大值 极差 标准差 1 1 1 1.000 1.000 1.000 1.000 0.000 − 2 5 15 1.880 1.900 1.680 2.000 0.320 0.093 3 8 36 2.883 2.893 2.673 2.993 0.320 0.075 4 8 36 3.895 3.905 3.730 3.970 0.240 0.058 5 7 28 4.926 4.935 4.800 5.000 0.200 0.048 6 5 15 5.935 5.938 5.867 5.987 0.120 0.031 7 3 6 6.956 6.958 6.923 6.983 0.060 0.022 8 2 3 7.975 7.975 7.965 7.985 0.020 0.010 9 1 1 8.991 8.991 8.991 8.991 0.000 − 10 1 1 10.000 10.000 10.000 10.000 0.000 − 总计 41 142 说明：−表示标准差缺失，仅有1个数值无法进行标准差计算
下载: 导出CSV
表 4 针阔混交林样地均匀度指数值
Table 4. Uniformity index values of coniferous and broad-leaved mixed forest
变量名 ISCD-U Simpson均匀
度指数Shannon均匀
度指数Alatalo均匀
度指数均值 0.808 0.801 0.722 0.730 中位数 0.824 0.829 0.737 0.742 方差 0.007 0.013 0.012 0.010 标准差 0.086 0.112 0.111 0.102 标准误 0.005 0.006 0.006 0.006 最小值 0.361 0.052 0.091 0.339 最大值 0.968 0.992 0.994 0.992 极差 0.607 0.940 0.903 0.652
下载: 导出CSV
表 5 均匀度指数之间的相关系数
Table 5. Correlation coefficient between uniformity indexes
均匀度指标 ISCD-U Simpson
均匀度指数Shannon
均匀度指数Alatalo
均匀度指数ISCD-U 1 Simpson
均匀度指数0.840** 1 Shannon
均匀度指数0.825** 0.934** 1 Alatalo
均匀度指数0.555** 0.668** 0.622** 1 说明：**表示在0.01水平上相关极显著(双尾)
下载: 导出CSV
表 6 针阔混交林样地的多样性指数值
Table 6. Diversity index values of coniferous and broad-leaved mixed forest
变量名 ISCD Simpson多样
性指数修正Simpson
多样性指数Shannon多样
性指数Mclntosh多样
性指数Shannon多样性
幂指数Hill多样
性指数均值 7.774 0.688 1.228 1.456 0.499 4.576 3.635 中位数 7.776 0.712 1.243 1.468 0.509 4.341 3.467 方差 7.497 0.014 0.128 0.134 0.012 2.662 1.704 标准差 2.738 0.117 0.357 0.366 0.110 1.631 1.305 标准误 0.153 0.007 0.020 0.020 0.006 0.091 0.073 最小值 1.724 0.035 0.035 0.100 0.019 1.106 1.036 最大值 16.860 0.870 2.044 2.291 0.727 9.889 7.719 极差 15.136 0.836 2.009 2.191 0.708 8.783 6.684
下载: 导出CSV
表 7 多样性指数之间的相关系数
Table 7. Correlation coefficient between diversity indexes
多样性指标 ISCD Simpson多样
性指数修正Simpson
多样性指数Shannon多样
性指数Mclntosh多样
性指数Shannon多样性
幂指数Hill多样
性指数ISCD 1 Simpson多样性指数 0.684** 1 修正Simpson多样性指数 0.724** 0.967** 1 Shannon多样性指数 0.839** 0.943** 0.965** 1 Mclntosh多样性指数 0.635** 0.967** 0.965** 0.929** 1 Shannon多样性幂指数 0.840** 0.878** 0.952** 0.974** 0.891** 1 Hill多样性指数 0.719** 0.891** 0.975** 0.934** 0.914** 0.967** 1 说明：**表示在0.01水平上相关极显著(双尾)
下载: 导出CSV
-
[1] 亢新刚. 森林经理学[M]. 4版. 北京: 中国林业出版社, 2011. KANG Xingang. Forest Management[M]. 4 ed. Beijing: China Forestry Publishing House, 2011. [2] 陈云, 王婷, 李培坤, 等. 河南木札岭温带落叶阔叶林群落特征及主要乔木空间分布格局[J]. 植物生态学报, 2016, 40(11): 1179 − 1188. CHEN Yun, WANG Ting, LI Peikun, et al. Community characteristics and spatial distribution of dominant tree species in a deciduous broad-leaved forest of Muzhaling, Henan, China [J]. Chin J Plant Ecol, 2016, 40(11): 1179 − 1188. [3] 胡跃华, 曹敏, 林露湘. 西双版纳热带季节雨林的树种组成和群落结构动态[J]. 生态学报, 2010, 30(4): 949 − 957. HU Yuehua, CAO Min, LIN Luxiang. Dynamics of tree species composition and community structure of a tropical seasonal rain forest in Xishuangbanna, Southwest China [J]. Acta Ecol Sin, 2010, 30(4): 949 − 957. [4] 姜萍, 赵光, 叶吉, 等. 长白山北坡森林群落结构组成及其海拔变化[J]. 生态学杂志, 2003, 22(6): 28 − 32. JIANG Ping, ZHAO Guang, YE Ji, et al. Structure of forest communities on the northern slope of Changbai Mountain and its variation along elevation gradients [J]. Chin J Ecol, 2003, 22(6): 28 − 32. [5] 周君璞, 郑小贤. 将乐林场栲类次生林物种组成与多样性研究[J]. 中南林业科技大学学报, 2014, 34(10): 70 − 75. ZHOU Junpu, ZHENG Xiaoxian. Study on species composition and species diversity of Castanopsis secondary forest in Jiangle forest farm [J]. J Cent South Univ For Technol, 2014, 34(10): 70 − 75. [6] 汤孟平, 唐守正, 李希菲, 等. 树种组成指数及其应用[J]. 林业资源管理, 2003, 24(2): 33 − 36. TANG Mengping, TANG Shouzheng, LI Xifei, et al. Tree species composition index and its application [J]. For Resour Manage, 2003, 24(2): 33 − 36. [7] 王寿兵. 对传统生物多样性指数的质疑[J]. 复旦学报(自然科学版), 2003, 42(6): 867 − 868. WANG Shoubing. A question on the traditional biodiversity index [J]. J Fudan Univ Nat Sci, 2003, 42(6): 867 − 868. [8] 赵中华, 惠刚盈. 林分结构多样性研究进展[J]. 林业科学, 2020, 56(9): 143 − 152. ZHAO Zhonghua, HUI Gangying. Advances in structural diversity of stand structure [J]. Sci Silv Sin, 2020, 56(9): 143 − 152. [9] 雷相东, 唐守正. 林分结构多样性指标研究综述[J]. 林业科学, 2002, 38(3): 140 − 146. LEI Xiangdong, TANG Shouzheng. Indicators on structural diversity within-stand: a review [J]. Sci Silv Sin, 2002, 38(3): 140 − 146. [10] 周彬, 郑小贤, 钟艳, 等. 林分物种多样性指标体系的研究[J]. 北京林业大学学报, 2002, 24(2): 24 − 28. ZHOU Bin, ZHENG Xiaoxian, ZHONG Yan, et al. Synthetic indices for stand species diversity [J]. J Beijing For Univ, 2002, 24(2): 24 − 28. [11] 张金屯. 植被数量生态学方法[M]. 北京: 中国科学技术出版社, 1995. ZHANG Jintun. Quantitative Ecology[M]. Beijing: Science and Technology of China Press, 1995. [12] 许晴, 张放, 许中旗, 等. Simpson指数和Shannon-Wiener指数若干特征的分析及“稀释效应”[J]. 草业科学, 2011, 28(4): 527 − 531. XU Qing, ZHANG Fang, XU Zhongqi, et al. Some characteristics of Simpson index and the Shannon-Wiener index and their dilution effect [J]. Pratacultural Sci, 2011, 28(4): 527 − 531. [13] ALATALO R V. Problems in the measurement of evenness in ecology [J]. Oikos, 1981, 37(2): 199 − 204. [14] 唐守正, 郎奎建, 李海奎. 统计和生物数学模型计算: ForStat教程[M]. 北京: 中国科学技术出版社, 2009. TANG Shouzheng, LANG Kuijian, LI Haikui. Statistical and Biomathematical Model Calculations: ForStat Tutorial[M]. Beijing: Science and Technology of China Press, 2009. [15] KEMPTON R A. The structure of species abundance and measurement of diversity [J]. Biometrics, 1979, 35(1): 307 − 321. [16] MCINTOSH R P. An index of diversity and the relation of certain concepts to diversity [J]. Ecology, 1967, 48(3): 392 − 404. [17] CAO Y, HAWKINS C P. Weighting effective number of species measures by abundance weakens detection of diversity responses [J]. J Appl Ecol, 2019, 56(5): 1200 − 1209. [18] KEYLOCK C J. Simpson diversity and the Shannon-Wiener index as special cases of a generalized entropy [J]. Oikos, 2005, 109(1): 203 − 207. [19] JOST L. Entropy and diversity [J]. Oikos, 2006, 113(2): 363 − 375. [20] STIRLING G, WILSEY B. Empirical relationships between species richness, evenness, and proportional diversity [J]. Am Nat, 2001, 158(3): 286 − 299. [21] WILSEY B J, CHALCRAFT D R, BOWLES C M, et al. Relationships among indices suggest that richness is an incomplete surrogate for grassland biodiversity [J]. Ecology, 2005, 86(5): 1178 − 1184. [22] HURLBERT S H. The nonconcept of species diversity: a critique and alternate parameters [J]. Ecology, 1971, 52(4): 577 − 586. [23] MACDONALD Z G, NIELSEN S E, ACORN J H. Negative relationships between species richness and evenness render common diversity indices inadequate for assessing long-term trends in butterfly diversity [J]. Biodiversity Conserv, 2017, 26(3): 617 − 629. [24] HILL M O. Diversity and evenness: a unifying notation and its consequences [J]. Ecology, 1973, 54(2): 427 − 432. [25] PIERSON K. Building a richer understanding of diversity through causally consistent evenness measures [J]. Ecol Evol, 2020, 10(20): 10965 − 10973. [26] SU Qiang. A relationship between species richness and evenness that depends on specific relative abundance distribution[J/OL]. PeerJ, 2018, 6: e4951[2020-12-08]. doi: 10.7717/peerj.4951. [27] TUOMISTO H. An updated consumer’s guide to evenness and related indices [J]. Oikos, 2012, 121(8): 1203 − 1218. [28] 娄明华, 白超, 惠刚盈, 等. 7个林木大小多样性指数表达能力比较[J]. 生物多样性, 2019, 27(4): 449 − 456. LOU Minghua, BAI Chao, HUI Gangying, et al. Comparison of distinguish ability on seven tree size diversity indices [J]. Biodiversity Sci, 2019, 27(4): 449 − 456. 期刊类型引用(4)
1. 张泽宇，朱明喜，陈昊泽，刘明源，张紫微，郑威. 龙眼DlFNS蛋白的生物信息学分析. 分子植物育种. 2024(01): 61-67 . 
百度学术2. 杨欣蓉，于旭东，吴繁花，蔡泽坪，罗佳佳，曹佩娜. 菠萝蜜BRI1家族成员生物信息学的预测与对比. 分子植物育种. 2021(01): 100-110 . 百度学术3. 宋丽娟，陈冬丽，李留振. 探究几种核桃花芽分化规律及分化时间. 天津农林科技. 2019(02): 37-38 . 百度学术4. 张云婷，江雷雨，叶云天，冯琛，孙勃，王小蓉，汤浩茹. 草莓FaCOP1的克隆及其表达特异性分析. 园艺学报. 2017(03): 547-556 . 百度学术其他类型引用(1)
-
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20210171
点击查看大图
计量
- 文章访问数: 1175
- HTML全文浏览量: 399
- PDF下载量: 65
- 被引次数: 5
