Age structure and spatial point pattern of Phoebe sheareri population in Mount Tianmu

天目山国家级自然保护区(30°18′30″~30°24′55″N，119°24′11″~119°28′21″E)地处浙江省西北部，位于杭州市临安区境内。景区内天目山主峰——仙人顶海拔1 506 m，总面积约4 284 hm²。年平均降水量为1 390~1 870 mm，年平均气温为8.8~14.8 ℃。该自然保护区森林植被丰茂、生物多样性较高。天目山的紫楠种群主要分布在海拔800 m以下区域，由于保护区严格管理，人类活动的痕迹较少，生长状况接近自然状态。

2012年8月在浙江省天目山国家级自然保护区选择典型常绿阔叶林，建立1块1 hm² (100 m×100 m)动态监测研究样地。样地地理位置位于30°19′48.360″N，119°26′9.546″E，海拔为588.98 m。将样地的西南角作为直角坐标系的原点，自西向东为坐标系的横轴，由南向北为坐标系的纵轴，使用南方测绘NTS-300R全站仪将整个样地划分为25个20 m×20 m的小样方，于2018年6月对样地内胸径≥1.0 cm的每株木本植物进行定位测量，记录物种名称、胸径、高度、冠幅、枝下高、生长状况等特征。调查发现，样地内共有木本植物90种，共计2 282株，主要树种见表1。

以紫楠个体的胸径作为代表紫楠树龄的指标^[15]。参照林木径级结构的划分标准，按胸径(D_BH)定义为5个径级，即径级1、径级2、径级3、径级4、径级5。样地内紫楠种群结构特征见表2。

存活曲线是以种群存活数量的对数值为纵坐标，以年龄为横坐标，把每个种群的死亡和存活情况绘成1条曲线，反映物种个体从幼体到老年所能存活的比率。一般可分为3种基本类型：①DeeveyⅠ型。曲线凸型，表示该种群幼体存活率高，老年个体存活率低，生命周期结束前只有少数个体死亡；②DeeveyⅡ型。曲线呈对角线型，表示该种群在整个生存周期中保持了稳定的死亡率；③DeeveyⅢ型。曲线凹型，表示该种群幼体死亡率较高^[16]。

1977年RIPLEY^[7]第1次使用统计学理论描述点格局分析法。1983年DIGGLE^[17]将点格局分析归纳总结为函数K(t)：

式(1)中：t表示空间尺度；$\lambda $表示某一植物个体数在单位面积上的均值；K(t)表示从某一点起，距离t内的期望点数。DIGGLE^[17]在实践中，提出了K(t)的估计值$\hat K(t)$：

式(2)中：A表示样地平面面积；n为总点数(某径级的植物立木个体数)；${u_{i,j}}$表示i、j 2个不同个体之间的直线距离，${u_{i,j}} {\text{≤} }t$时，$I({u_{i,j}})$=1；${u_{i,j}} $＞t时，$I({u_{i,j}})$=0；${W_{i,j}}$表示以某株植物$i$为圆心，${u_{i,j}}$为半径的圆在样地中的圆弧与整个圆周长的比例。在式(2)中引入${W_{i,j}}$来消除样地边界带来的影响。

在随机分布情况下，$\sqrt {\hat K(t)/{\text{π}} } $和$t$呈正比，故引入新的参数$H(t)$：

式(3)中：$H(t)$表示点格局与空间尺度$t$的关系。在随机分布下，任何空间尺度t下的$H(t)$恒等于0；$H(t)$＞0表示植物种群在空间内集群分布；$H(t) $＜0表示植物种群在空间内均匀分布。

在众多零假设模型中，本研究使用完全空间随机模型(CSR)对函数$H(t)$的值进行检验。用蒙特卡洛方法可以拟合出一组随机分布的植物种群空间分布坐标，以此计算在任意$t$下的$H(t)$。重新拟合一组坐标，可以得到一组新的$H(t)$值。拟合次数达到一定次数时，从多种$H(t)$中选出不同$t$下$H(t)$的最大值和最小值。分别将最大值和最小值连接成2条曲线，包迹线曲线所包含的区域即为随机分布的置信区间。若$H(t)$在包迹线内，则表明物种是随机分布的；若$H(t)$在包迹线外，则物种是明显偏离了随机分布。大量的实践表明，若要置信区间的可信度大于95%时，则至少需要拟合20次；若要大于99%，则至少需要拟合100次。

考虑不同径级的植物个体在$t$内的数目，${\hat K_{p,q}}(t)$的计算原理与式(2)相似，为：

式(4)中：${\hat K_{p,q}}(t)$ 表示径级 $p$ 和径级 $q$ 之间的K(t)估计值($p$=1，2，3，4，5；$q$=1，2，3，4，5，且 $p \ne q$)；${n_p}$ 表示径级 $p$ 的植物个体数；${n_q}$ 表示径级 $q$ 的植物个体数，如果下标为2, 3，则表示径级2与径级3之间的K(t)估计值，依次类推；其他参数的含义与式(2)相同。则 ${H_{p,q}}(t)$ 为：

式(5)中：${H_{p,q}}(t)$表示径级$p$与径级$q$之间的点格局与空间尺度$t$之间的关系，其他同理类推。

本研究使用蒙特卡洛方法检验不同径级之间的关联性。首先，分别拟合出2组随机分布的植物种群空间分布坐标，植株数量与同一径级所包含的植株数量相同；其次，通过式(4)和式(5)计算任意t下的${H_{p,q}}(t)$；然后，再次拟合出2组坐标，重复计算任意t下的${H_{p,q}}(t)$，共拟合20次；最后，从20条曲线中选取不同尺度t下的最大值(最小值)，连接全部最大值(最小值)，得到上(下)包迹线。

假设2个径级之间的曲线大于上包迹线，则为显著正关联；小于上包迹线，则无显著关联。假设2个径级之间的曲线小于下包迹线，则为显著负关联；大于下包迹线，则无显著关联。由大量的实践经验可知：使用蒙特卡洛方法拟合20次的置信区间可信度大于95%。

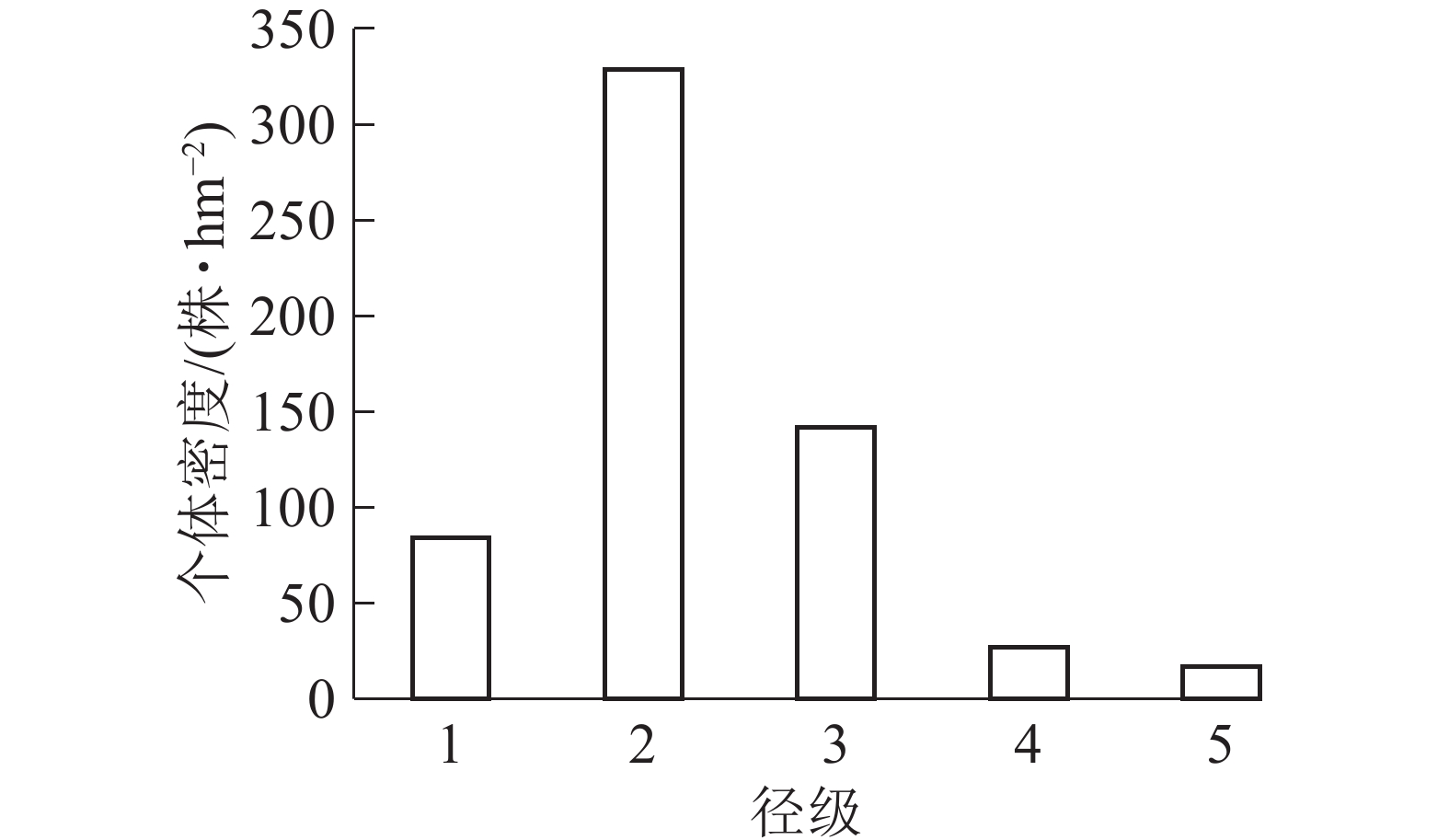
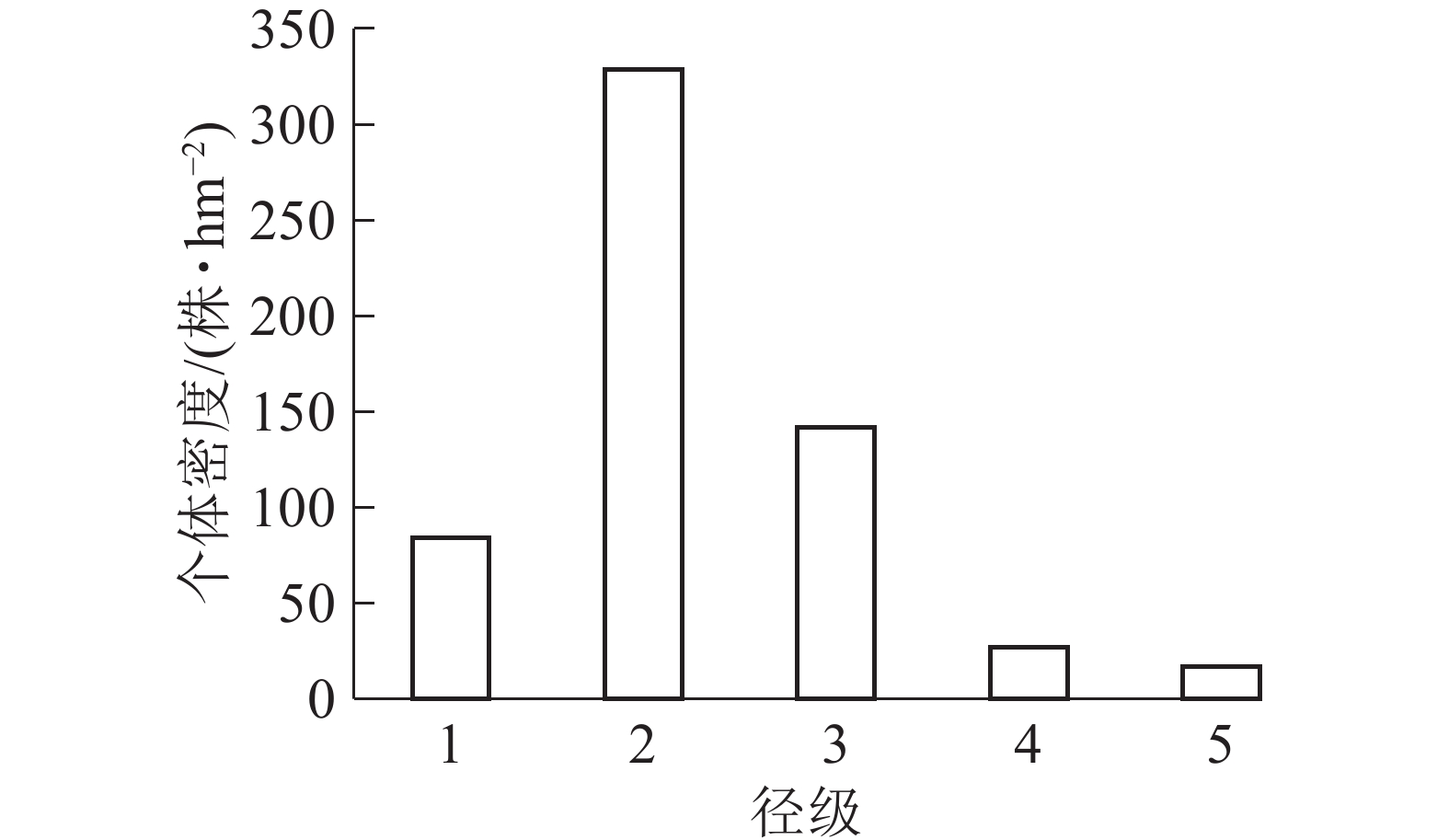
样地内紫楠合计599株，占调查木本植物总数的26.25%。如图1所示：个体密度径级1为84株·hm⁻²，占14.02%；径级2为329株·hm⁻²，占54.92%；径级3为142株·hm⁻²，占25.40%；径级4为27株·hm⁻²，占4.83%；径级5为17株·hm⁻²，占3.04%。

Figure 1.  Number of individuals of different diameter classes in the plot

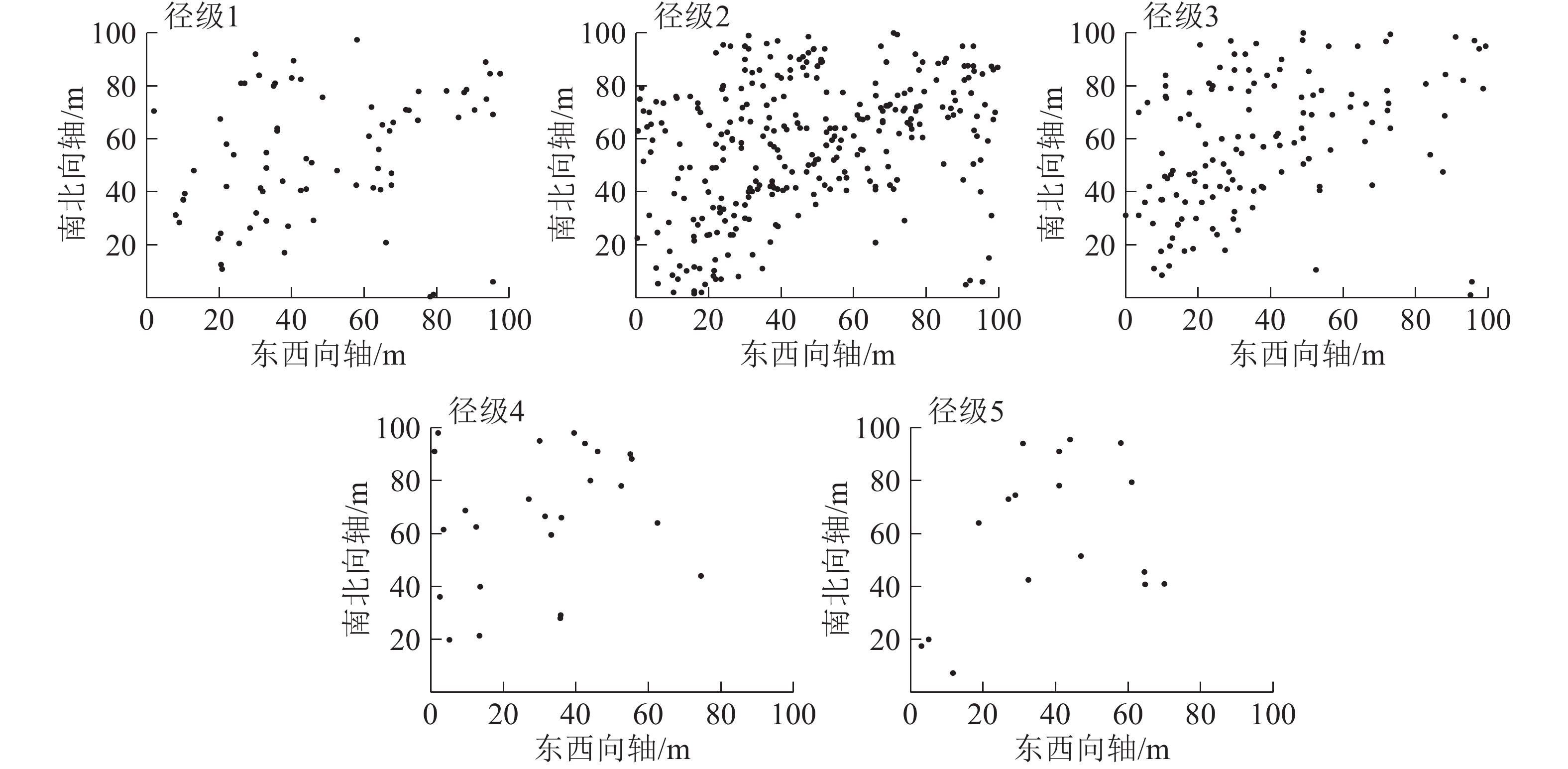
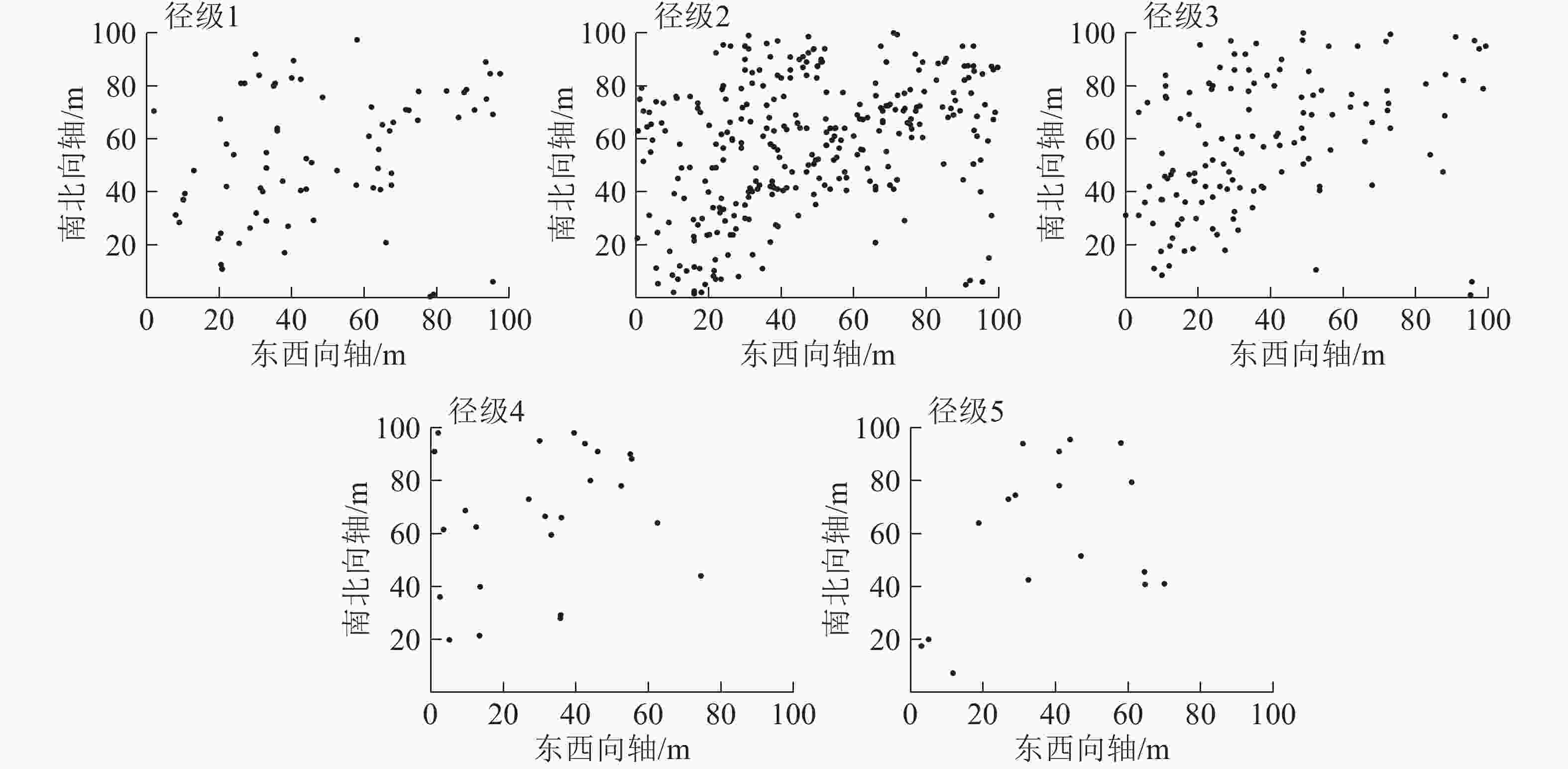
从图2可见：5个径级紫楠个体在100 m×100 m样地内的空间分布密度，从大到小依次为径级2、径级3、径级1、径级4、径级5。

Figure 2.  Individual spatial distribution of different diameter classes in the plot

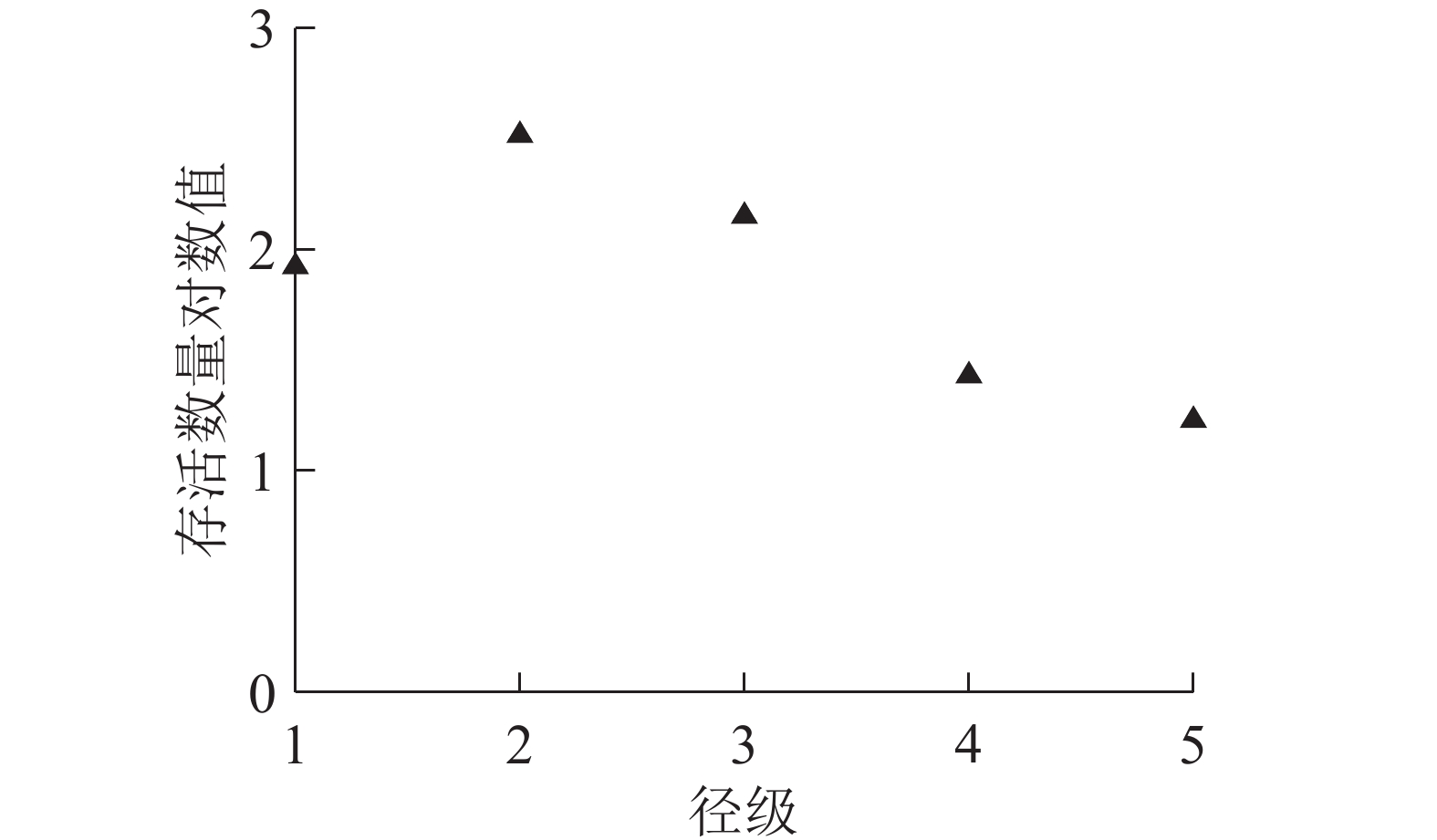
制作紫楠种群的存活曲线(图3)时，以径级为横轴，存活数量对数值为纵轴。参照Deevey存活曲线与紫楠种群的存活曲线比较发现：紫楠种群的存活曲线介于Deevey Ⅰ和Ⅱ型曲线之间，靠近Deevey Ⅰ型。说明紫楠种群在接近生理寿命之前只有少数个体死亡。

Figure 3.  Population survivorship curve of P. sheareri

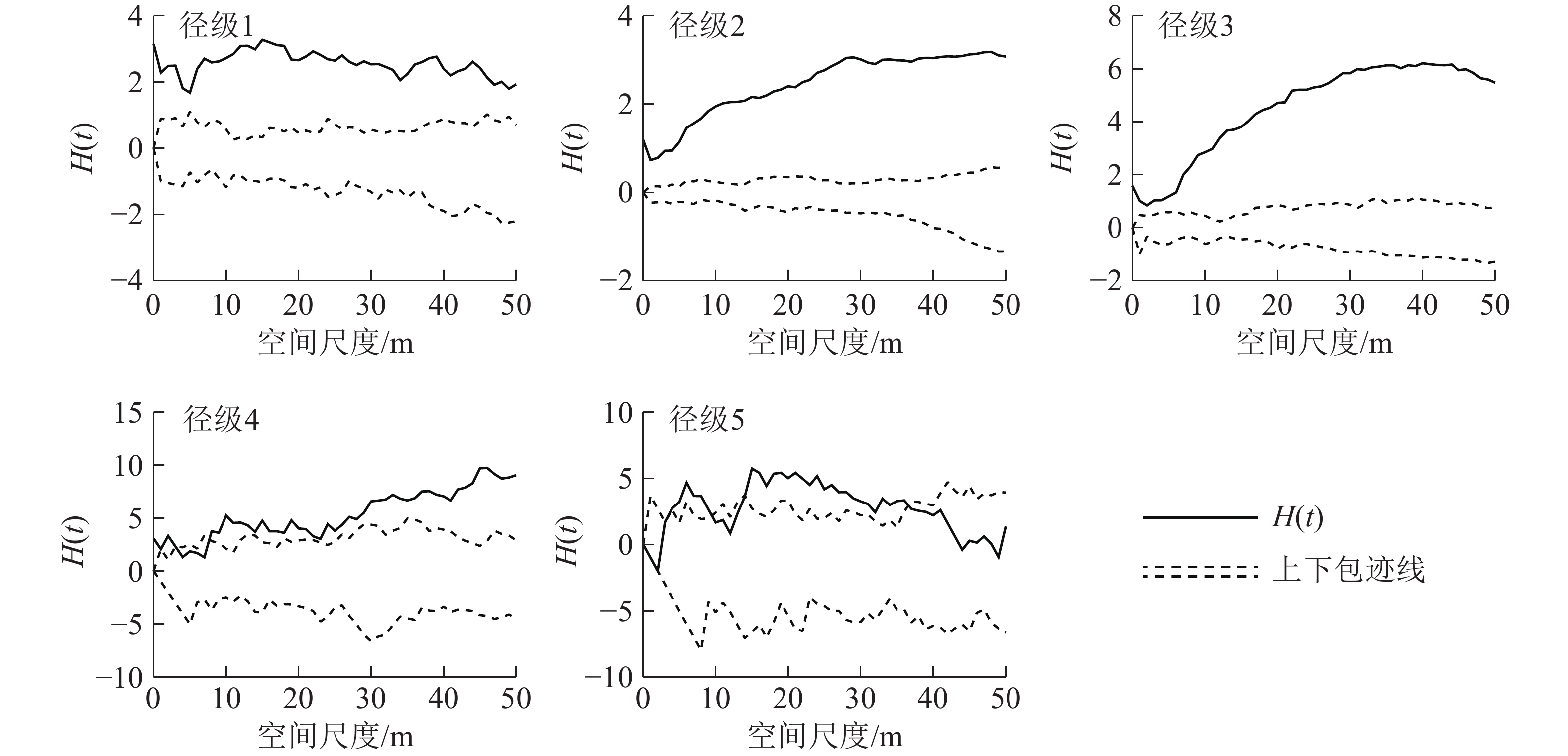
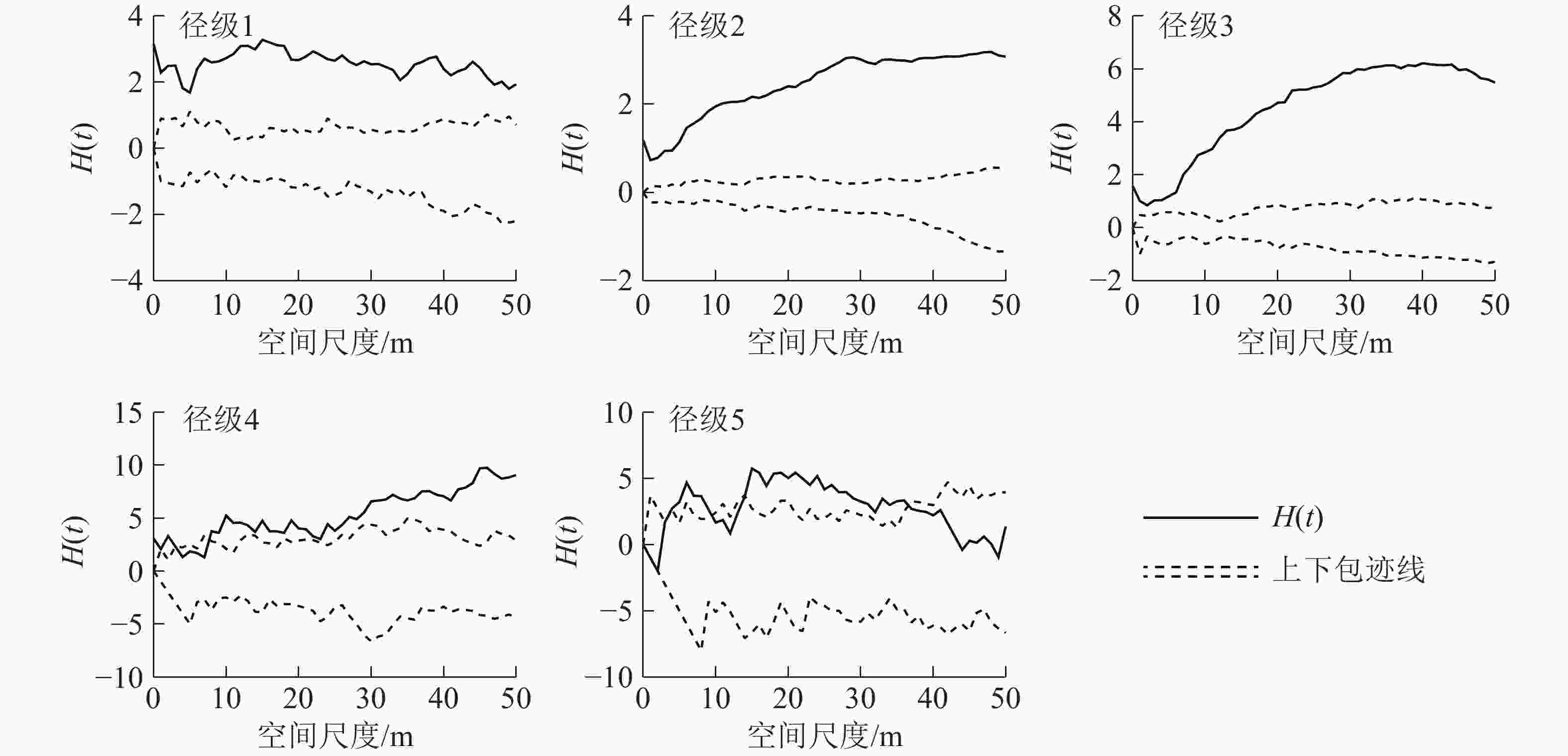
如图4所示：使用CSR假设模型对样地内紫楠种群进行点格局分析，径级2、径级3、径级4阶段植株的H(t)函数取值在整个尺度内呈增长趋势。径级1和径级5阶段植株的H(t)函数取值在大尺度内减小。

Figure 4.  Point pattern analysis of various diameter classes

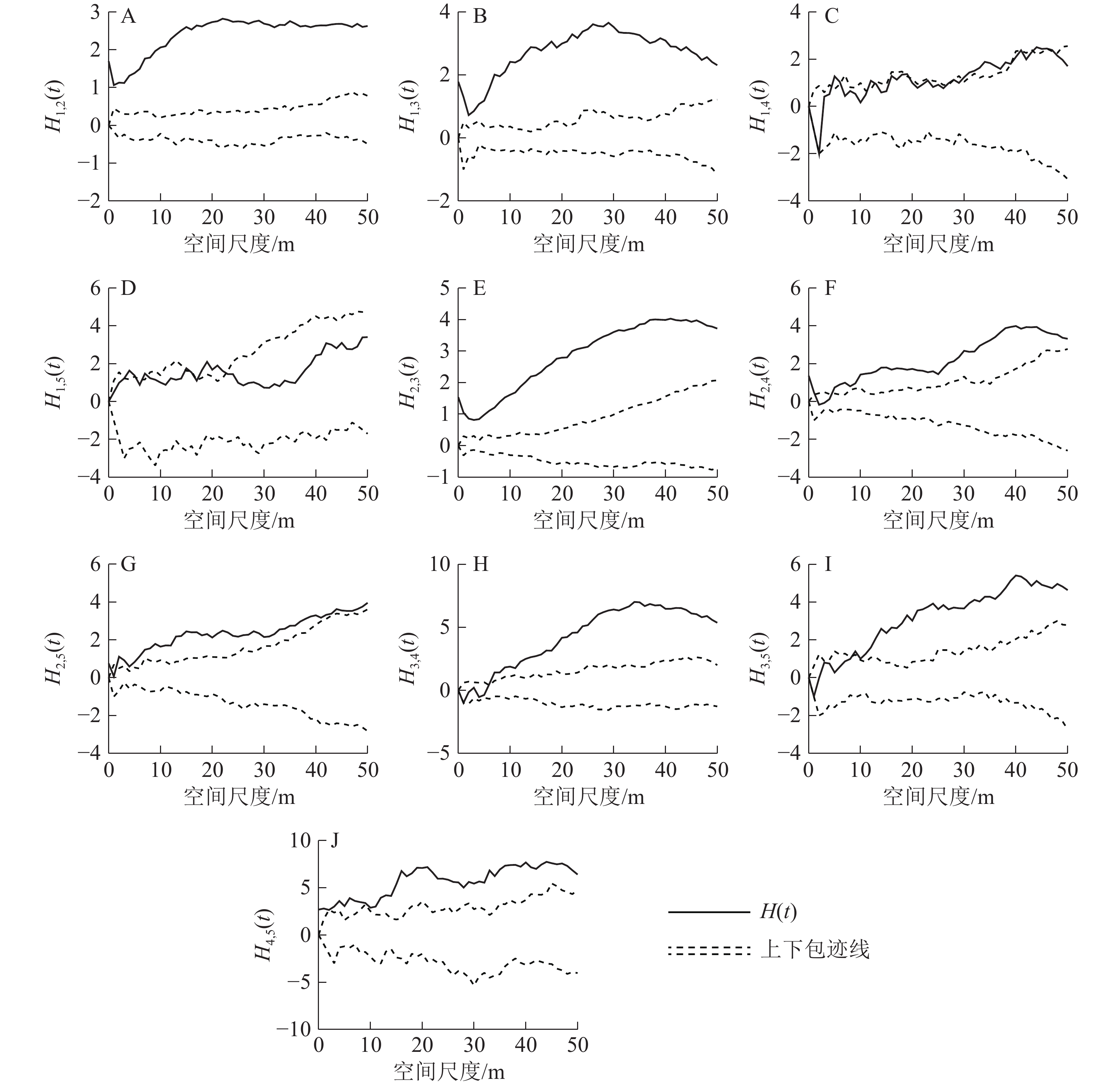
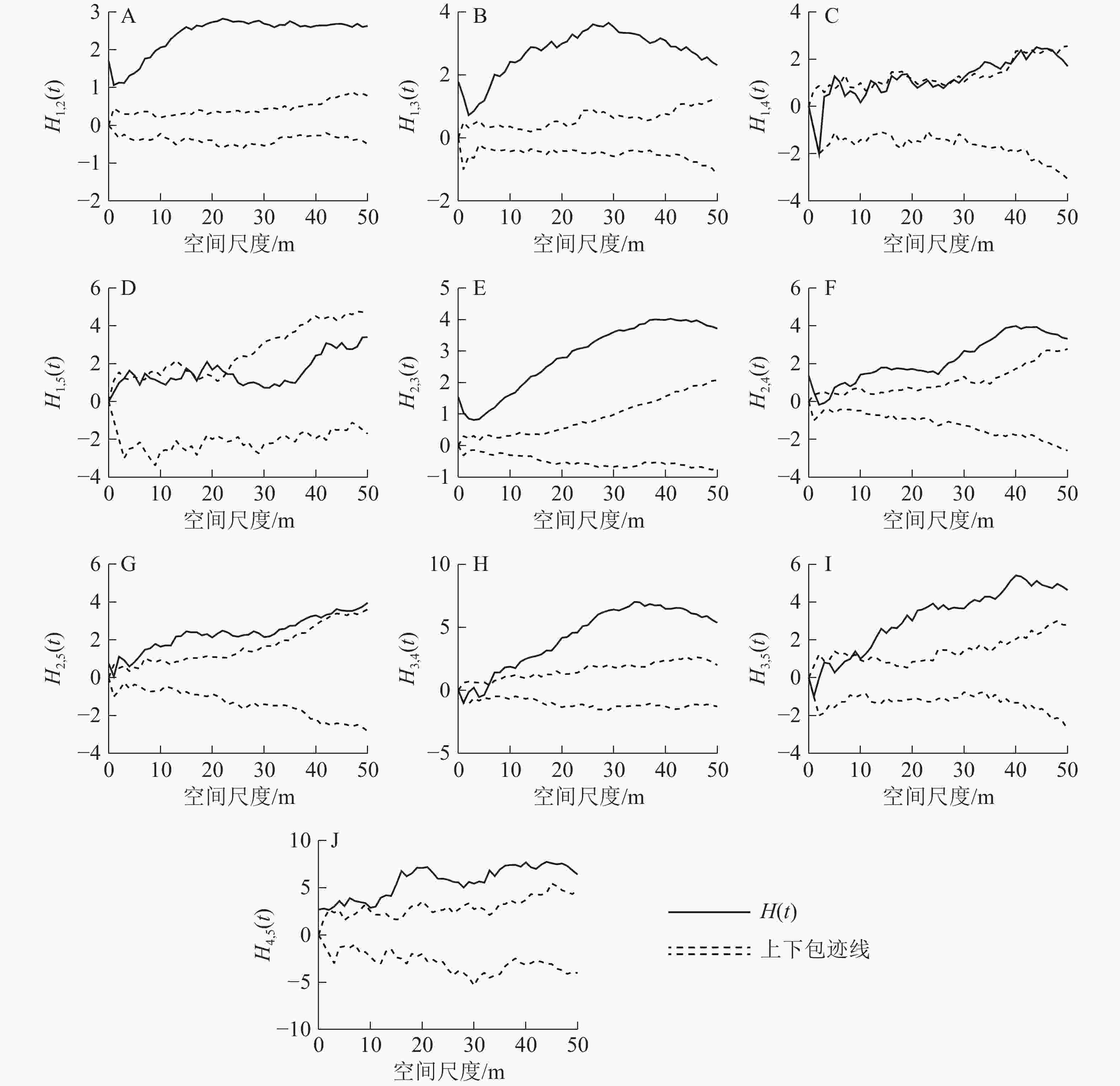
径级1和径级2之间呈显著的正关联关系(图5A)。径级1和径级3个体在小尺度接近显著的正关联水平，之后随着尺度的增大，正关联性也越大(图5B)。径级1和径级4个体随着尺度由小到大从接近显著负关联水平逐渐过渡到无关联，再到接近显著正关联水平(图5C)。两者在0~3 m尺度下达显著负关联水平，在3~6 m尺度下两者无关联，在6~50 m尺度内两者达到或者接近显著正关联水平。径级1和径级5个体在小尺度内两者接近显著正关联水平，在大尺度内两者无显著关联(图5D)。在所有尺度下，径级2和径级3的正关联性十分显著(图5E)。在小尺度内，径级2和径级4无显著关联；在9~50 m尺度内，两者为显著正关联关系(图5F)。在小尺度内，径级2和径级5之间的关系达到或者接近显著正关联水平；随着尺度增大，两者的正关联度越大，在35~50 m大尺度内正关联度又下降，恢复到接近显著正关联水平(图5G)。在小尺度内，径级3和径级4接近显著负关联水平；在尺度2~6 m内，两者无显著关联；在尺度6~50 m内，两者为显著正关联(图5H)。在小尺度内，径级3和径级5同样接近显著负关联水平；在2~4 m尺度内，则无显著关联性；在尺度4~14 m内的关联曲线与上包迹线在大部分尺度下互相交错，关联达到或者接近显著正关联水平，在尺度14~50 m之内，两者为显著正关联(图5I)。径级4和径级5在0~12 m尺度下达到或者接近显著正关联水平；在尺度12~50 m内为显著正关联(图5J)。

Figure 5.  Point pattern analysis between different diameter classes

从天目山紫楠种群年龄结构来看，低龄(即径级1、径级2)个体数占样方内紫楠总统计量的68.95%。其次是中龄个体(径级3)，占23.71%，高龄(即径级4、径级5)个体树木比较少，占7.34%。各径级比例符合增长性种群的年龄结构变化规律，种群内存在着大量可以用来更新换代的幼苗和幼树，且靠近Deevey I型的存活曲线也说明了其大多数个体能活到平均的生理寿命。因此，天目山紫楠种群属于增长型的发展模式。

天目山紫楠种群各径级都呈集群分布，其中径级1、径级2、径级3尤其明显。主要原因如下：①紫楠属耐阴树种。健康的紫楠种子呈圆润的椭圆形状，有一定的质量，主要通过重力和动物传播。种子成熟后掉落，通常都聚集在以母株为中心的范围内，或是聚集在动物巢穴周围。除此之外，老年个体也会通过根部萌孽产生新个体。②植物为了提高种群的生存和竞争力，低龄个体在水分、阳光、土壤等生态因子以及与别的种群的竞争中处于劣势地位，聚集可以提高其竞争能力和对不良环境的抵御能力。③小生境的异质作用，如环境因子的差异，包括局部的土壤、地形、植被等。同一物种不同个体对生长所需要的环境条件要求在大体上是具有一致性的。所以小生境的异质性也会致使幼树相对集群分布。

随着树龄的增长，紫楠个体聚集度逐渐降低，并趋向随机分布。引起这种变化主要是受到生物学特征以及环境资源限制使种内和种间竞争日益凸显的影响。例如径级4、径级5个体树冠基本定型，根系已足够发达，对各种资源(阳光、水分、土壤等)的需求也愈大。随着个体的不断成熟，出现自疏效应，因此高龄个体集群分布显著度逐渐降低。

同一物种不同生长阶段的个体在空间分布上的相互关联性，是对一定时期内组成植物种群个体之间相互关系的描述。这种关系不仅是指空间分布关系，也包含了个体间的功能关系，反映种群内个体间的相互作用^[18−19]。

天目山紫楠径级1、径级2、径级3在所有尺度内都呈显著正关联，并且随着尺度的增大关联性愈大。由于紫楠主要以种子和高龄个体根部萌孽繁殖，但低龄、中龄个体在生长过程中与高龄个体在资源的获取上出现竞争。大径级紫楠个体的树荫不利于小径级幼龄紫楠个体的生长，尤其在小尺度下阻碍作用更明显。因此低龄、中龄与高龄个体在小尺度上无显著关联，甚至出现负关联，但在大尺度上多数个体仍然为正关联，例如径级2和径级4，径级1和径级5等。

高龄个体为了争夺生存空间，存在着相互排斥的生态关系，因此在一定范围内无显著关联。虽然高龄个体存在竞争关系，但对环境的要求具有一致性。空间上的交错分布有利于充分利用资源，也有利于整个种群在种间竞争中取得优势，因此高龄个体在大尺度上处于正关联状态。综上所述，种群不同生长阶段个体的分布格局、关联性是种群和群落与环境长期相互作用的结果，是种群结构、群落结构合理性的体现^[20−21]。

种群空间分布格局具有尺度变异性，这种性质受到多种因素的制约，例如种内或种间竞争^[13]、生境的异质性和斑块性等^[22−24]。在本研究中天目山紫楠种群低龄和中龄个体主要呈现集群分布特征；高龄个体从集群分布逐渐趋向于随机分布。这一现象主要与紫楠的生物学特性还有种内种间竞争有关。天目山自然保护区环境的均匀性、干扰程度、历史等因素差异都不突出，因此紫楠各径级间关系密切，以正关联为主。